题目内容
在等比数列{an}中,首项a1<0,则{an}是递增数列的充要条件是公比( )
| A、q>1 | B、q<1 |
| C、0<q<1 | D、q<0 |
考点:等比数列的性质
专题:综合题,等差数列与等比数列
分析:先证必要性,由首项小于0,数列为递增数列,可得公比q大于0,得到数列的各项都小于0,利用等比数列的性质化简
,得到其比值为q,根据其比值小于1,得到公比q小于1,综上,得到满足题意的q的范围;再证充分性,由0<q<1,首项为负数,得到数列各项都为负数,利用等比数列的性质化简
,得到其比值为q,根据q小于1,得到an+1>an,即数列为递增数列,综上,得到{an}是递增数列的充要条件是公比q满足0<q<1,得到正确的选项.
| an+1 |
| an |
| an+1 |
| an |
解答:
解:先证必要性:
∵a1<0,且{an}是递增数列,
∴an<0,即q>0,且
=q<1,则此时等比q满足0<q<1,
再证充分性:
∵a1<0,0<q<1,
∴an<0,
∴
=q<1,即an+1>an,则{an}是递增数列,
综上,{an}是递增数列的充要条件是公比q满足0<q<1.
故选C.
∵a1<0,且{an}是递增数列,
∴an<0,即q>0,且
| an+1 |
| an |
再证充分性:
∵a1<0,0<q<1,
∴an<0,
∴
| an+1 |
| an |
综上,{an}是递增数列的充要条件是公比q满足0<q<1.
故选C.
点评:此题考查了等比数列的性质,通项公式,以及充要条件的证明,熟练掌握等比数列的性质是解本题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
已知α为锐角,且满足cos2α=sinα,则α等于( )
| A、30°或270° | B、45° |
| C、60° | D、30° |
若log2x•log34•log59=8,则x=( )
| A、8 | B、25 | C、16 | D、4 |
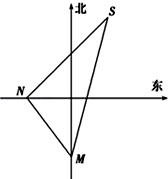 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为