题目内容
若直线ax+by+c=0(ab≠0)在两坐标轴上的截距相等,则a,b,c满足的条件是( )
| A、a=b |
| B、|a|=|b| |
| C、c=0或a=b |
| D、c=0或|a|=|b| |
考点:直线的截距式方程
专题:直线与圆
分析:当c=0时,直线ax+by+c=0(ab≠0)过原点,在两坐标轴上的截距相等,当c≠0时,直线在两坐标轴上的截距分别为-
和-
,由题意可得-
=-
,故a=b,由此得出结论.
| c |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
解答:
解:当c=0时,直线ax+by+c=0(ab≠0)过原点,在两坐标轴上的截距相等.
当c≠0时,直线在两坐标轴上的截距分别为-
和-
,由题意可得-
=-
,故a=b.
综上,当c=0或c≠0且a=b时,直线ax+by+c=0(ab≠0)在两坐标轴上的截距相等,
故选C.
当c≠0时,直线在两坐标轴上的截距分别为-
| c |
| b |
| c |
| a |
| c |
| b |
| c |
| a |
综上,当c=0或c≠0且a=b时,直线ax+by+c=0(ab≠0)在两坐标轴上的截距相等,
故选C.
点评:本题主要考查直线的一般式方程,直线在两坐标轴上的截距的定义,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
对于函数f(x)定义域中任意的x1,x2(x1≠x2)有如下结论
①f(x1+x2)=f(x1)•f(x2);
②f(x1•x2)=f(x1)+f(x2);
③
<0;
④f(
)>
.
当f(x)=lnx时,上述结论中正确的序号是( )
①f(x1+x2)=f(x1)•f(x2);
②f(x1•x2)=f(x1)+f(x2);
③
| f(x1)-f(x2) |
| x1-x2 |
④f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
当f(x)=lnx时,上述结论中正确的序号是( )
| A、①③ | B、②③ | C、②④ | D、③④ |
已知α为锐角,且满足cos2α=sinα,则α等于( )
| A、30°或270° | B、45° |
| C、60° | D、30° |
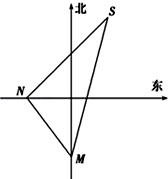 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为