题目内容
在平面直角坐标系xOy中,已知点A(2,2),B(0,4),圆C以线段AB为直径
(1)求圆C的方程;
(2)设点P是圆C上与点A不重合的一点,且OP=OA,求直线PA的方程和△POA的面积.
(1)求圆C的方程;
(2)设点P是圆C上与点A不重合的一点,且OP=OA,求直线PA的方程和△POA的面积.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)确定圆心与半径,即可求圆C的方程;
(2)利用点斜式可得直线PA的方程,求出PA,点O到直线PA的距离,可求△POA的面积.
(2)利用点斜式可得直线PA的方程,求出PA,点O到直线PA的距离,可求△POA的面积.
解答:
解:(1)设圆C的圆心C(a,b),半径为r,则a=1,b=3---------(2分)
r=AC=
=
--------------------------------------------(4分)
∴圆C的方程为(x-1)2+(y-3)2=2----------------------------------------(6分)
(2)∵OP=OA,CP=CA,∴OC是线段PA的垂直平分线---------------(8分)
又OC的斜率为3,∴PA的斜率为-
------------------------------------------(9分)
∴直线PA的方程为y-2=-
(x-2),即x+3y-8=0-----------------(10分)
∵点O到直线PA的距离d=
=
-------------------------------(11分)
OA=
=2
…..(12分)
∴PA=2
=2
=
…(13分)
∴△POA的面积=
PA•d=
×
×
=
…(14分)
r=AC=
| (2-1)2+(2-3)2 |
| 2 |
∴圆C的方程为(x-1)2+(y-3)2=2----------------------------------------(6分)
(2)∵OP=OA,CP=CA,∴OC是线段PA的垂直平分线---------------(8分)
又OC的斜率为3,∴PA的斜率为-
| 1 |
| 3 |
∴直线PA的方程为y-2=-
| 1 |
| 3 |
∵点O到直线PA的距离d=
| |0+0-8| | ||
|
4
| ||
| 5 |
OA=
| 22+22 |
| 2 |
∴PA=2
| OA2-d2 |
8-(
|
4
| ||
| 5 |
∴△POA的面积=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 5 |
4
| ||
| 5 |
| 16 |
| 5 |
点评:本题考查直线和圆的方程的应用,考查圆的方程,考查三角形面积的计算,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
对于函数f(x)定义域中任意的x1,x2(x1≠x2)有如下结论
①f(x1+x2)=f(x1)•f(x2);
②f(x1•x2)=f(x1)+f(x2);
③
<0;
④f(
)>
.
当f(x)=lnx时,上述结论中正确的序号是( )
①f(x1+x2)=f(x1)•f(x2);
②f(x1•x2)=f(x1)+f(x2);
③
| f(x1)-f(x2) |
| x1-x2 |
④f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
当f(x)=lnx时,上述结论中正确的序号是( )
| A、①③ | B、②③ | C、②④ | D、③④ |
已知α为锐角,且满足cos2α=sinα,则α等于( )
| A、30°或270° | B、45° |
| C、60° | D、30° |
若log2x•log34•log59=8,则x=( )
| A、8 | B、25 | C、16 | D、4 |
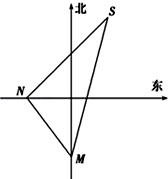 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为