题目内容
设a>0,b>0.若2a•2b=2,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| A、8 | ||
| B、4 | ||
| C、1 | ||
D、
|
考点:基本不等式,有理数指数幂的化简求值
专题:不等式的解法及应用
分析:首先将已知等式化简,得到a+b=1,再所求乘以a+b,展开,利用基本不等式求最小值.
解答:
解:因为2a•2b=2,所以2a+b=21,所以a+b=1,
因为a>0,b>0.则
+
=(a+b)(
+
)=2+
+
≥2+2=4,当且仅当
=
即a=b=
时等号成立;
故选B.
因为a>0,b>0.则
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| 1 |
| 2 |
故选B.
点评:本题考查了运用基本不等式求代数式的最小值;关键是1的巧用.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
不等式ax2+bx+2>0的解集是{x|-
<x<
},则a-b的值为( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、14 | B、-14 |
| C、10 | D、-10 |
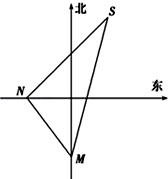 如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为
如图,一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的东北方向,则货轮的速度为