题目内容
已知数列{an}和{bn}满足:a1=λ,an+1=
an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
(1)对任意实数λ,求证:a1,a2,a3不成等比数列;
(2)试判断数列{bn}是否为等比数列,并证明你的结论.
| 2 |
| 3 |
(1)对任意实数λ,求证:a1,a2,a3不成等比数列;
(2)试判断数列{bn}是否为等比数列,并证明你的结论.
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:(1)假设存在一个实数λ,使a1,a2,a3是等比数列,由等比中项的概念列式得到矛盾的等式,说明假设错误,结论得到证明;
(2)由递推式bn=(-1)n(an-3n+21)得到bn+1,进一步得到bn+1=-
bn,求出b1=-(λ+18),
由此可知当λ≠-18时,数列{bn}是以-(λ+18)为首项,-
为公比的等比数列.
(2)由递推式bn=(-1)n(an-3n+21)得到bn+1,进一步得到bn+1=-
| 2 |
| 3 |
由此可知当λ≠-18时,数列{bn}是以-(λ+18)为首项,-
| 2 |
| 3 |
解答:
(1)证明:假设存在一个实数λ,使a1,a2,a3是等比数列,则有a22=a1a3,
即(
λ-3)2=λ(
λ-4),整理得
λ2-4λ+9=
λ2-4λ,得到9=0,矛盾.
∴a1,a2,a3不成等比数列;
(2)解:∵bn=(-1)n(an-3n+21),
∴bn+1=(-1)n+1[an+1-3(n+1)+21]=(-1)n+1(
an-2n+14)
=
(-1)n(an-3n+21)=-
bn,
又b1=-(λ+18),
∴当λ=-18时,bn=b1=0,(n为正整数),此时{bn}不是等比数列;
当λ≠-18时,b1≠0,由上式可知bn≠0,
∴
=-
(n为正整数),
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-
为公比的等比数列.
即(
| 2 |
| 3 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
∴a1,a2,a3不成等比数列;
(2)解:∵bn=(-1)n(an-3n+21),
∴bn+1=(-1)n+1[an+1-3(n+1)+21]=(-1)n+1(
| 2 |
| 3 |
=
| 2 |
| 3 |
| 2 |
| 3 |
又b1=-(λ+18),
∴当λ=-18时,bn=b1=0,(n为正整数),此时{bn}不是等比数列;
当λ≠-18时,b1≠0,由上式可知bn≠0,
∴
| bn+1 |
| bn |
| 2 |
| 3 |
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-
| 2 |
| 3 |
点评:本题考查了数列递推式,考查了等比关系的确定及等比数列的性质,体现了分类讨论的数学思想方法,是中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
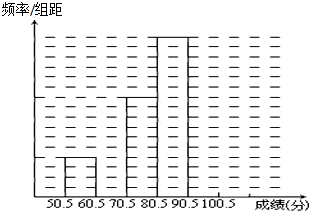 某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.从中抽取了部分学生的成绩进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题: 已知椭圆
已知椭圆