题目内容
10.设函数f(x)=x•lnx+ax,a∈R.(Ⅰ)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求函数y=f(x)在$[\frac{1}{e},e]$上的最小值;
(Ⅲ)若$g(x)=f(x)+\frac{1}{2}a{x^2}-(2a+1)x$,求证:a≥0是函数y=g(x)在x∈(1,2)时单调递增的充分不必要条件.
分析 (Ⅰ)求出函数的导数,计算f(1),f′(1),求出切线方程即可;
(Ⅱ)求出f(x)的最小值,通过讨论a的范围,得到函数f(x)的单调性,从而确定f(x)在闭区间的最小值即可;
(Ⅲ)求出g(x)的导数,通过讨论a的范围分别证明充分性和必要性即可.
解答 解:(Ⅰ)由f(x)=xlnx+ax得:f′(x)=lnx+a+1.
当a=1时,f′(x)=lnx+2,f(1)=1,f′(1)=2,
求得切线方程为y=2x-1…(4分)
(Ⅱ)令f′(x)=0,得x=e-(a+1),
∴当e-(a+1)≤$\frac{1}{e}$,即a≥0时,x∈[$\frac{1}{e}$,e]时f′(x)≥0恒成立,f(x)单调递增,
此时f(x)min=f($\frac{1}{e}$)=$\frac{a-1}{e}$.
当e-(a+1)≥e,即a≤-2时,x∈[$\frac{1}{e}$,e]时,f′(x)≤0恒成立,f(x)单调递减,
此时f(x)min=f(e)=ae+e,
当$\frac{1}{e}$<e-(a+1)<e,即-2<a<0时,x∈[$\frac{1}{e}$,e-(a+1))时,f′(x)<0,f(x)单减;
x∈(e-(a+1),e)时,f′(x)>0,f(x)单增,此时f(x)min=f(e-(a+1))=-e-(a+1),
…(9分)
(Ⅲ)g′(x)=f′(x)+ax-(2a+1)=lnx+a(x-1),
∴当a≥0时,x∈(1,2)时lnx>0,a(x-1)≥0,g′(x)>0恒成立,
函数y=g(x)在x∈(1,2)时单调递增,充分条件成立;
又当a=-$\frac{1}{2}$时,代入g′(x)=lnx-$\frac{1}{2}$x+$\frac{1}{2}$,
设h(x)=g′(x)=lnx-$\frac{1}{2}$x+$\frac{1}{2}$,x∈(1,2),
则h′(x)=$\frac{2-x}{2x}$>0恒成立
∴当x∈(1,2)时,h(x)单调递增.
又h(1)=0,∴当x∈(1,2)时,h(x)>0恒成立.
而h(x)=g′(x),
∴当x∈(1,2)时,g′(x)>0恒成立,函数y=g(x)单调递增.
∴必要条件不成立
综上,a≥0是函数y=g(x)在x∈(1,2)时单调递增的充分不必要条件.…(14分)
点评 本题考查了充分必要条件,考查函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.

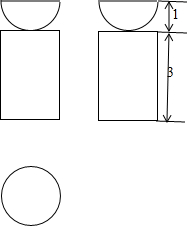 如图是一个组合体的三视图,根据图中数据,可得该几何体的体积是( )
如图是一个组合体的三视图,根据图中数据,可得该几何体的体积是( )| A. | $\frac{38π}{3}$ | B. | $\frac{19π}{3}$ | C. | $\frac{13π}{3}$ | D. | $\frac{11π}{3}$ |