题目内容
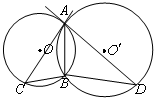如图，⊙O和⊙O′都经过A，B两点，AC是⊙O′的切线，交⊙O于点C，AD是⊙O的切线，交⊙O′于点D，求证：AB2=BC•BD．考点：与圆有关的比例线段
专题：立体几何
分析：由已知条件得△ACB∽△DAB，由此能证明AB2=BC•BD．
解答：
（本小题满分为8分）
证明：因为AC是⊙O的切线，AD是⊙O′的切线，
所以∠1=∠C，∠2=∠D，（3分）
所以△ACB∽△DAB，（4分）
故
=
，（6分）
所以AB2=BC•BD．（8分）
（本小题满分为8分）证明：因为AC是⊙O的切线，AD是⊙O′的切线，
所以∠1=∠C，∠2=∠D，（3分）
所以△ACB∽△DAB，（4分）
故
| BC |
| AB |
| AB |
| BD |
所以AB2=BC•BD．（8分）
点评：本题考查AB2=BC•BD的证明，是中档题，解题时要认真审题，注意三角形相似的性质的灵活运用．
练习册系列答案
53随堂测系列答案
相关题目
等差数列{an}，a7-2a4=-1，且a3=0，则公差d=（ ）
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
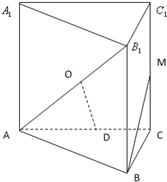已知直三棱柱ABC-A1B1C1的底面△ABC中，∠C=90°，BC=