题目内容
等差数列{an},a7-2a4=-1,且a3=0,则公差d=( )
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:根据条件和的等差数列的通项公式性质列出关于d的方程求出d.
解答:
解:∵a7-2a4=-1,且a3=0,
∴a3+4d-2(a3+d)=-1,
解得d=-
.
故选B.
∴a3+4d-2(a3+d)=-1,
解得d=-
| 1 |
| 2 |
故选B.
点评:本题考查了等差数列的通项公式的灵活应用,属于基础题.

练习册系列答案
相关题目
已知b>0,则“ab2<b”是“ab<1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知实数x>y,且y≠0,则下列结论正确的是( )
A、
| ||||
| B、cx>cy(c∈R) | ||||
| C、x3>y3 | ||||
D、
|
在等差数列{an}中,已知a1=
,a4+a5=
,若an=33,则n=( )
| 1 |
| 3 |
| 16 |
| 3 |
| A、50 | B、49 | C、48 | D、47 |
数列{an}前六项是1,2,4,8,16,它的一个通项公式是( )
| A、an=2n |
| B、an=2n |
| C、an=2n+1 |
| D、an=2n-1 |
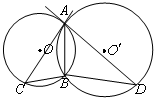 如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,求证:AB2=BC•BD.
如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,求证:AB2=BC•BD.