题目内容
已知函数f(x)=
+4(x≠0),各项均为正数的数列{an}中a1=1,
=f(an),(n∈N*).
(1)求数列{an}的通项公式;
(2)在数列{bn}中,对任意的正整数n,bn•
=1都成立,设Sn为数列{bn}的前n项和.试比较Sn与
的大小.
| 1 |
| x2 |
| 1 |
| an+12 |
(1)求数列{an}的通项公式;
(2)在数列{bn}中,对任意的正整数n,bn•
| (3n-1)an2+n |
| an2 |
| 1 |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件得
=
+4,由此能求出an=
.
(2)由已知得bn=
=
=
=
(
-
),由此利用裂项求和法能求出Sn=
-
<
.
| 1 |
| an+12 |
| 1 |
| an2 |
| 1 | ||
|
(2)由已知得bn=
| an2 |
| (3n-1)an2+n |
| ||
|
| 1 |
| 4n2-1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 4n+2 |
| 1 |
| 2 |
解答:
解:(1)∵数f(x)=
+4(x≠0),
各项均为正数的数列{an}中a1=1,
=f(an),
∴
=
+4,
∴
=1+(n-1)×4=4n-3,
∴an=
.
(2)∵bn•
=1,
∴bn=
=
=
=
(
-
),
∴Sn=
(1-
+
-
+…+
-
)
=
(1-
),
=
-
<
.
∴Sn<
.
| 1 |
| x2 |
各项均为正数的数列{an}中a1=1,
| 1 |
| an+12 |
∴
| 1 |
| an+12 |
| 1 |
| an2 |
∴
| 1 |
| an2 |
∴an=
| 1 | ||
|
(2)∵bn•
| (3n-1)an2+n |
| an2 |
∴bn=
| an2 |
| (3n-1)an2+n |
| ||
|
=
| 1 |
| 4n2-1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Sn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 4n+2 |
| 1 |
| 2 |
∴Sn<
| 1 |
| 2 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
已知实数x>y,且y≠0,则下列结论正确的是( )
A、
| ||||
| B、cx>cy(c∈R) | ||||
| C、x3>y3 | ||||
D、
|
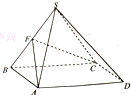 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知∠DAB=135°,BC=2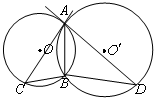 如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,求证:AB2=BC•BD.
如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,求证:AB2=BC•BD. 已知平面内一动点P到定点F(2,0)的距离与点P到y轴的距离的差等于2.
已知平面内一动点P到定点F(2,0)的距离与点P到y轴的距离的差等于2.