题目内容
7．
一个几何体的三视图如图所示，则该几何体的表面积为（ ）| A． | 4π+8 | B． | $\frac{4π}{3}$+24 | C． | 4π+24 | D． | $\frac{4π}{3}$+8 |
分析 几何体上部为球，下部为正方体．代入面积公式计算即可．
解答 解：由三视图可知几何体上部为半径为1的球，下部为棱长为2的正方体．
∴几何体的表面积S=4π×12+6×22=24+4π．
故选C．
点评 本题考查了常见几何体的三视图与表面积计算，属于基础题．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
17．两个分类变量X与Y有关系的可能性越大，随机变量K2的值（ ）
| A． | 越大 | B． | 越小 | ||
| C． | 不变 | D． | 可能越大也可能越小 |
18．
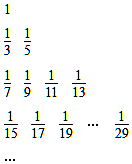把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图，第k行有2k-1个数，第t行的第s个数（从左数起）记为A（t，s），则A（6，10）=（ ）
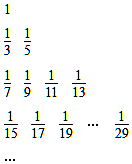把数列{$\frac{1}{2n-1}$}的所有数按照从大到小的原则写成如图，第k行有2k-1个数，第t行的第s个数（从左数起）记为A（t，s），则A（6，10）=（ ）| A． | $\frac{1}{99}$ | B． | $\frac{1}{87}$ | C． | $\frac{1}{81}$ | D． | $\frac{1}{85}$ |
15．在极坐标系中，点$（4，\frac{π}{3}）$到直线$ρsin（θ-\frac{π}{3}）=2$的距离是（ ）
| A． | 2 | B． | 3 | C． | $\sqrt{2}$ | D． | 1 |
2．
将正奇数1，3，5，7，…排成五列（如表），按此表的排列规律，2017所在的位置是（ ）
将正奇数1，3，5，7，…排成五列（如表），按此表的排列规律，2017所在的位置是（ ）| A． | 第一列 | B． | 第二列 | C． | 第三列 | D． | 第四列 |
12．
某几何体的三视图如图所示，其中俯视图是半圆，则该几何体的体积为（ ）
某几何体的三视图如图所示，其中俯视图是半圆，则该几何体的体积为（ ）| A． | $\frac{\sqrt{3}}{6}$π | B． | $\frac{3}{2}$π | C． | $\frac{1}{6}$π | D． | $\frac{\sqrt{3}}{3}$π |
3．已知3sin2α+2sin2β=1，3sin2α-2sin2β=0，且α、β都是锐角，则α+2β的值为（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{π}{3}$ | D． | $\frac{π}{4}$ |