题目内容
若(x2-
)n展开式的二项式系数之和为32,则展开式中含x4的项的系数是( )
| 1 |
| x |
| A、10 | B、-10 | C、-5 | D、5 |
考点:二项式定理的应用
专题:二项式定理
分析:先根据二项式系数的性质求得n=5,可得二项式展开式的通项公式,再令x的幂指数等于4,求得r的值,即可求得展开式中含x4的项的系数.
解答:
解:由(x2-
)n展开式的二项式系数之和为2n=32,求得n=5,
可得(x2-
)n展开式的通项公式为 Tr+1=
•(-1)r•x10-3r,
令10-3r=4,求得 r=2,则展开式中含x4的项的系数是
=10,
故选:A.
| 1 |
| x |
可得(x2-
| 1 |
| x |
| C | r 5 |
令10-3r=4,求得 r=2,则展开式中含x4的项的系数是
| C | 2 5 |
故选:A.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
为了得到函数y=3cos2x的图象,只需把函数y=3sin(2x+
)的图象上所有的点( )
| π |
| 6 |
A、向右平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向左平行移动
|
已知命题:若数列{an}为等差数列,且am=a,an=b(m≠n,m、n∈N+)则am+n=
;现已知等比数列{bn}(bn>0,n∈N+),bm=a,bn=b,(m≠n,m、n∈N+)若类比上述结论,则可得到bm+n=( )
| bn-am |
| n-m |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
某校高二共有8个班,现有10个三好生名额需分配到各班,每班至少1个名额的分配方法有( )种.
| A、16 | B、24 | C、36 | D、64 |
三棱锥P-ABC中,AB=BC=2,AB⊥BC,PA⊥底面ABC,且PA=2,则此三棱锥外接球的半径为( )
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
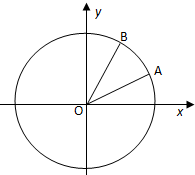 如图,在平面直角坐标系xOy中,以Ox轴为始边,两个锐角α,β的终边分别与单位圆相交于A,B 两点.
如图,在平面直角坐标系xOy中,以Ox轴为始边,两个锐角α,β的终边分别与单位圆相交于A,B 两点.