题目内容
已知⊙C1的方程为x2+y2=1,⊙C2的方程为(x-2)2+(y-2)2=5,求过点P(0,1)与⊙C1、C2截得的弦长相等的直线方程.
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:设直线方程为y=kx+1,即kx-y+1=0,利用过点P(0,1)与⊙C1、C2截得的弦长相等,建立方程,求出k,即可求过点P(0,1)与⊙C1、C2截得的弦长相等的直线方程.
解答:
解:设直线方程为y=kx+1,即kx-y+1=0,
∵过点P(0,1)与⊙C1、C2截得的弦长相等,
∴1-(
)2=5-(
)2,
解得:k=-1,
∴直线方程为x+y-1=0.
∵过点P(0,1)与⊙C1、C2截得的弦长相等,
∴1-(
| 1 | ||
|
| |2k-1| | ||
|
解得:k=-1,
∴直线方程为x+y-1=0.
点评:本题考查直线与圆的位置关系,考查弦长的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
三棱锥S-ABC的4个顶点和6条棱的中点共有10个点,其中4点共面有m组,从m组中任取一组,取到含点S组的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 淮北市某小区为了解居民对“小区物业管理”的满意度,现随机抽取
淮北市某小区为了解居民对“小区物业管理”的满意度,现随机抽取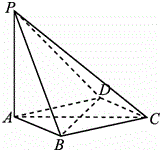 如图,在四棱椎P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱椎P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°. 如图程序框图表示求
如图程序框图表示求