题目内容
2.已知:函数f(x)=$\frac{{2}^{x}-{2}^{-x}}{2}$,g(x)=$\frac{{2}^{x}+{2}^{-x}}{2}$.(1)求证:f(x+y)=f(x)g(y)+f(y)g(x);
(2)试讨论函数g(x)的奇偶性与单调性.
分析 (1)根据指数幂的运算法则进行化简即可.
(2)根据函数奇偶性和单调性的定义进行判断即可.
解答 解:(1)∵f(x)=$\frac{{2}^{x}-{2}^{-x}}{2}$,g(x)=$\frac{{2}^{x}+{2}^{-x}}{2}$.
∴f(y)=$\frac{{2}^{y}-{2}^{-y}}{2}$,g(y)=$\frac{{2}^{y}+{2}^{-y}}{2}$,
则f(x)g(y)+f(y)g(x)=$\frac{{2}^{x}-{2}^{-x}}{2}$•$\frac{{2}^{y}+{2}^{-y}}{2}$+$\frac{{2}^{x}+{2}^{-x}}{2}$•$\frac{{2}^{y}-{2}^{-y}}{2}$
=$\frac{{2}^{x}{2}^{y}+{2}^{x}{2}^{-y}-{2}^{-x}{2}^{y}-{2}^{-x}{2}^{-y}}{4}$+$\frac{{2}^{x}{2}^{y}-{2}^{x}{2}^{-y}+{2}^{-x}{2}^{y}-{2}^{-x}{2}^{-y}}{4}$
=$\frac{2({2}^{x}{2}^{y}-{2}^{-x}{2}^{-y})}{4}$=$\frac{{2}^{x+y}-{2}^{-(x+y)}}{2}$,
∵f(x+y)=$\frac{{2}^{x+y}-{2}^{-(x+y)}}{2}$.
∴f(x+y)=f(x)g(y)+f(y)g(x);
(2)∵g(-x)=$\frac{{2}^{-x}+{2}^{x}}{2}$=$\frac{{2}^{x}+{2}^{-x}}{2}$=g(x),
∴函数g(x)为偶函数,
当x≥0时,设0≤x1<x2,
则g(x1)-g(x2)=$\frac{1}{2}$(${2}^{{x}_{1}}$+${2}^{-{x}_{1}}$-${2}^{{x}_{2}}$-${2}^{-{x}_{2}}$)
=$\frac{1}{2}$(${2}^{{x}_{1}}$-${2}^{{x}_{2}}$+$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{{2}^{{x}_{1}}{2}^{{x}_{2}}}$)
=$\frac{1}{2}$(${2}^{{x}_{1}}$-${2}^{{x}_{2}}$)•$\frac{{2}^{{x}_{1}}{2}^{{x}_{2}}-1}{{2}^{{x}_{1}}{2}^{{x}_{2}}}$,
∵0≤x1<x2,
∴1≤${2}^{{x}_{1}}$<${2}^{{x}_{2}}$,
则${2}^{{x}_{1}}$-${2}^{{x}_{2}}$<0,${2}^{{x}_{1}}$•${2}^{{x}_{2}}$>1•
则g(x1)-g(x2)<0,
即g(x1)<g(x2),
即函数g(x)在[0,+∞)上为增函数,
则函数g(x)在(-∞,0]为减函数.
点评 本题主要考查函数式的证明以及函数奇偶性和单调性的判断,利用指数幂的运算法则以及函数奇偶性和单调性的定义是解决本题的关键.运算量比较大.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案| A. | m≤-1 | B. | m<-1 | C. | m≤-2015 | D. | m<-2015 |
| A. | 0 | B. | 4 | C. | 12 | D. | 10 |
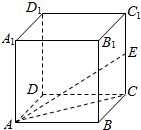
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | 2$\sqrt{2}$ |
| A. | (5,7) | B. | (4,6) | C. | (5,9) | D. | (4,7) |
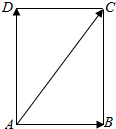 一艘货船从A点出发,以v km/h的速度向垂直于岸边DC的方向行驶,同时河水的流速为2km/h,河水流动的方向为$\overrightarrow{AB}$,货船实际航行的方向为$\overrightarrow{AC}$,而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$,求v.
一艘货船从A点出发,以v km/h的速度向垂直于岸边DC的方向行驶,同时河水的流速为2km/h,河水流动的方向为$\overrightarrow{AB}$,货船实际航行的方向为$\overrightarrow{AC}$,而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$,求v.