题目内容
3．小明每天步行上学，途中要走过几条街道，假设街道之间是平行或垂直的，小明走出家门口直行50米后右转直行50米，之后左转直行100米后再右转直行100米到达学校，则小明家与学校的直线距离是（ ）| A． | 100$\sqrt{2}$米 | B． | 120$\sqrt{2}$米 | C． | 150$\sqrt{3}$米 | D． | 150$\sqrt{2}$米 |
分析 由题意作出图形，利用数形结合思想能求出小明家与学校的直线距离．
解答 
解：如图，设小明家在A点，学校在E点，
由题意，AB=BC=50米，CD=DE=100米，AB⊥BC，CD⊥DE，
∴小明家与学校的直线距离是：
AE=AC+CE=$\sqrt{5{0}^{2}+5{0}^{2}}+\sqrt{10{0}^{2}+10{0}^{2}}$=150$\sqrt{2}$米．
故选：D．
点评 本题考查小明家与学校的直线距离的求法，是基础师，解题时要认真审题，注意数形结合思想的合理运用．
练习册系列答案
相关题目
13．已知圆Г过点（1，1）、（1，3）、（2，2），P是圆Г的一个动点，若A（-3，4），O为坐标原点，则$\overrightarrow{OP}$•$\overrightarrow{OA}$的最大值为（ ）
| A． | 0 | B． | 4 | C． | 12 | D． | 10 |
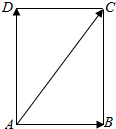一艘货船从A点出发，以v km/h的速度向垂直于岸边DC的方向行驶，同时河水的流速为2km/h，河水流动的方向为$\overrightarrow{AB}$，货船实际航行的方向为$\overrightarrow{AC}$，而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$，求v．
15．若x＞0，则下面式子中最小值等于6的是（ ）
| A． | x+$\frac{16}{x}$ | B． | x2+$\frac{16}{x}$ | C． | x+$\frac{32}{{x}^{2}}$ | D． | x+$\frac{36}{x}$ |