题目内容
求抛物线y=x2在A（1，1）处的切线，并求出切线与y轴及该抛物线所围成的图形面积．
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：求出函数的切线方程，利用积分的几何意义即可求出区域的面积．
解答：
解：函数的导数为f′（x）=2x，
则在（1，1）处的切线斜率k=f′（1）=1，
则对应的切线方程为y-1=2（x-1），即y=2x-1，
则由积分的几何意义可得阴影部分的面积S=
（x2-2x+1）dx=（
x3-x2+x）
=
．
则在（1，1）处的切线斜率k=f′（1）=1，
则对应的切线方程为y-1=2（x-1），即y=2x-1，
则由积分的几何意义可得阴影部分的面积S=
| ∫ | 1 0 |
| 1 |
| 3 |
| | | 1 0 |
| 1 |
| 3 |
点评：本题主要考查导数的应用，利用导数的几何意义求出切线方程，以及利用积分求区域面积是解决本题的关键．
练习册系列答案
相关题目
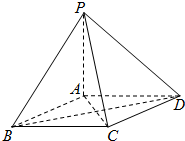如图，四棱锥P-ABCD的俯视图是菱形ABCD，顶点P的投影恰好为A．
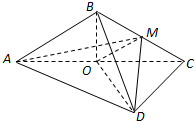菱形ABCD的边长为3，AC与BD交于O，且∠BAD=60°．将菱形ABCD沿对角线AC折起得到三棱锥B-ADC（如图），点M是棱BC的中点，DM=