题目内容
已知函数f(x)=lg((x-1)|ax-1|),
(a∈R)在其定义域上为单调函数,则a的取值范围是 .
(a∈R)在其定义域上为单调函数,则a的取值范围是
考点:函数单调性的判断与证明
专题:计算题,分类讨论,函数的性质及应用,不等式的解法及应用
分析:对a讨论,当a=0时,当a<0时,当a>0时,结合复合函数的单调性:同增异减,异减一次函数和二次函数的单调性,即可得到a的取值范围.
解答:
解:函数f(x)=lg((x-1)|ax-1|),
由(x-1)|ax-1|>0,
当a=0时,解得x>1,则f(x)=lg(x-1)在x>1上递增,成立;
当a<0时,定义域为(1,+∞),f(x)=lg(x-1)(1-ax),
令t=(x-1)(1-ax)=-ax2+(a+1)x-1,在x>1递增,由y=lgt递增,可得f(x)递增,成立;
当a>0时,由(x-1)|ax-1|>0,解得x>1且x≠
,
当x≥
时,(x-1)|ax-1|=(x-1)(ax-1),若
>1,在x>1不为单调函数,
当
≤1,即a≥1,在x>1为递增函数;
当x<
时,y=(x-1)|ax-1|=(x-1)(1-ax),由于抛物线开口向下,在(1,
)先增后减,则不成立.
综上可得,a的取值范围是a≤0或a≥1.
故答案为:(-∞,0]∪[1,+∞).
由(x-1)|ax-1|>0,
当a=0时,解得x>1,则f(x)=lg(x-1)在x>1上递增,成立;
当a<0时,定义域为(1,+∞),f(x)=lg(x-1)(1-ax),
令t=(x-1)(1-ax)=-ax2+(a+1)x-1,在x>1递增,由y=lgt递增,可得f(x)递增,成立;
当a>0时,由(x-1)|ax-1|>0,解得x>1且x≠
| 1 |
| a |
当x≥
| 1 |
| a |
| 1 |
| a |
当
| 1 |
| a |
当x<
| 1 |
| a |
| 1 |
| a |
综上可得,a的取值范围是a≤0或a≥1.
故答案为:(-∞,0]∪[1,+∞).
点评:本题考查函数的单调性的运用,考查二次函数和对数函数的单调性的运用,考查分类讨论的思想方法,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
函数y=
•
的定义域为( )
| x-2 |
| x+5 |
| A、[一5,2] |
| B、(一∞,-5]U[2,+oo) |
| C、[一5,+∞) |
| D、[2,+∞) |
若函数f(x),g(x)分别是定义在R上的奇函数,则有( )
| A、f(0)=g(0) |
| B、f(0)>g(0) |
| C、f(0)<g(0) |
| D、无法比较 |
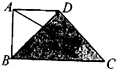 如图,在直角梯形ABCD中,DA=AB=1,BC=2,点P在阴影区域(含边界)中运动,则有
如图,在直角梯形ABCD中,DA=AB=1,BC=2,点P在阴影区域(含边界)中运动,则有| PA |
| BD |
A、[-
| ||
B、[-1,
| ||
| C、[-1,1] | ||
| D、[-1,0] |
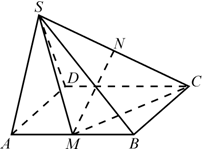 四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.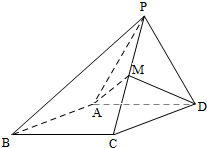 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.