题目内容
以下说法错误的是( )
| A、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |
| B、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| C、若命题p:?x0∈R,使得x02+x0+1<0,则﹁p:?x∈R,则x2+x+1≥0 |
| D、若p∨q为真命题,则p,q均为真命题 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:直接写出命题的逆否命题判断A正确;由充分条件、必要条件的概念判断B正确;直接写出特称命题的否定判断C正确;由复合命题的真假判断说明D错误.
解答:
解:对于A,命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”.
命题A正确;
对于B,由x=1,能够得到x2-3x+2=0.求解x2-3x+2=0得到x=1或x=2.
∴“x=1”是“x2-3x+2=0”的充分不必要条件.
命题B正确;
对于C,命题p:?x0∈R,使得x02+x0+1<0的否定为﹁p:?x∈R,则x2+x+1≥0.
命题C为真命题;
对于D,∵若p,q中只要有一个为真命题,则p∨q为真命题.
∴p∨q为真命题,则p,q均为真命题错误.
命题D为假命题.
故选:D.
命题A正确;
对于B,由x=1,能够得到x2-3x+2=0.求解x2-3x+2=0得到x=1或x=2.
∴“x=1”是“x2-3x+2=0”的充分不必要条件.
命题B正确;
对于C,命题p:?x0∈R,使得x02+x0+1<0的否定为﹁p:?x∈R,则x2+x+1≥0.
命题C为真命题;
对于D,∵若p,q中只要有一个为真命题,则p∨q为真命题.
∴p∨q为真命题,则p,q均为真命题错误.
命题D为假命题.
故选:D.
点评:本题考查了命题的真假判断与应用,解答的关键是熟记教材有关基础知识,属中档题.

练习册系列答案
相关题目
公比为2的等比数列{an}的各项都是正数,且a3a11=16,则log2a1=( )
| A、4 | B、-4 | C、2 | D、-2 |
函数f(x)=ln|x|(x≠0),则函数y=
+4f′(x)在(-∞,0)上的最大值是( )
| 1 |
| f′(x) |
| A、4 | B、-4 | C、2 | D、-2 |
函数y=
+
的值域是( )
| sinx |
| |sinx| |
| |cosx| |
| cosx |
| A、{-1,0,1,2} |
| B、{-2,0,2} |
| C、{-2,0} |
| D、{-2,2} |
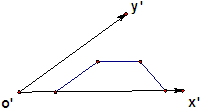 一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积等于( )
一个水平放置的平面图形的直观图是一个底角为45°,腰和上底长均为1的等腰梯形,则该平面图形的面积等于( )A、
| ||||||
B、1+
| ||||||
C、1+
| ||||||
D、2+
|
已知i是虚数单位,则复数z=i(2-i)所对应的点落在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
对任意的实数m,直线y=mx+1与圆x2+y2=4的位置关系一定是( )
| A、相切 |
| B、相交且直线过圆心 |
| C、相交且直线不过圆心 |
| D、相离 |
根据如图所示算法语句,当输入x为70时,输出y的值为( )


| A、25 | B、27 | C、35 | D、37 |