题目内容
10.若存在x0>1,使不等式(x0+1)ln x0<a(x0-1)成立,则实数a的取值范围是 ( )| A. | (-∞,2) | B. | (2,+∞) | C. | (1,+∞) | D. | (4,+∞) |
分析 若存在x0>1,使不等式(x0+1)ln x0<a(x0-1)成立,则存在x0>1,使不等式a>$\frac{({x}_{0}+1{)lnx}_{0}}{{x}_{0}-1}$成立,令f(x)=$\frac{{({x}_{\;}+1)lnx}_{\;}}{{x}_{\;}-1}$=(1+$\frac{2}{x-1}$)lnx,x>1,求出函数的极限,可得数a的取值范围.
解答 解:若存在x0>1,使不等式(x0+1)ln x0<a(x0-1)成立,
则存在x0>1,使不等式a>$\frac{({x}_{0}+1{)lnx}_{0}}{{x}_{0}-1}$成立,
令f(x)=$\frac{{({x}_{\;}+1)lnx}_{\;}}{{x}_{\;}-1}$=(1+$\frac{2}{x-1}$)lnx,x>1,
此时f(x)为增函数,
由$\lim_{x→1}f(x)$=$\lim_{x→1}lnx$+$\lim_{x→1}\frac{2lnx}{x-1}$=$\lim_{x→1}\frac{2lnx}{x-1}$→2
故a>2,
即实数a的取值范围是(2,+∞),
点评 本题考查的知识点是函数存在性问题,函数的单调性,极限运算,难度中档.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
19.已知数列{an}为等差数列,若a2+a6+a10=$\frac{π}{2}$,则tan(a3+a9)的值为( )
| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
16.点B是点A(1,2,3)在坐标平面yOz内的射影,则|OB|等于( )
| A. | $\sqrt{14}$ | B. | $\sqrt{13}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{10}$ |
15.已知△ABC的外接圆的圆心为O,AB=2,AC=3,BC=4,则$\overrightarrow{AO}$•$\overrightarrow{BC}$=( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 7 |
2.某校为了解高一年级学生身高情况,按10%的比例对全校700名高一学生按性别进行抽样检查,测得身高频数分布表如下:
表1:男生身高频数分布表
表2:女生身高频数分布表
则该校高一学生身高(单位:cm)在[165,180)的概率$\frac{4}{7}$.
表1:男生身高频数分布表
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 13 | 13 | 5 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 8 | 12 | 5 | 3 | 1 |
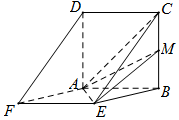 已知边长为2的正方形ABCD与菱形ABEF所在平面互相垂直,M为BC中点.
已知边长为2的正方形ABCD与菱形ABEF所在平面互相垂直,M为BC中点.