题目内容

已知sin（
π
2
+θ）=
3
7
，则cos2（
π
2
-θ）=
 
．
考点：同角三角函数基本关系的运用,二倍角的余弦
专题：三角函数的求值
分析：由题意可得cosθ=
3
7
，再根据cos2（
π
2
-θ）=sin2θ=1-cos2θ，计算求得结果．
解答： 解：∵sin（
π
2
+θ）=
3
7
=cosθ，则cos2（
π
2
-θ）=sin2θ=1-cos2θ=1-
9
49
=
40
49
，
故答案为：
40
49
．
点评：本题主要考查同角三角函数的基本关系、诱导公式的应用，属于中档题．
练习册系列答案
相关题目
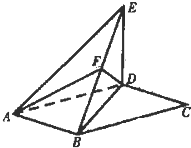如图，平行四边形ABCD中，∠DAB=60°，AB=2，AD=4；将△CBD沿BD折起到△EBD的位置，使平面EBD⊥平面ABD．
（1）求证：AB⊥DE；
（2）若点F为BE的中点，求直线AF与平面ADE所成角正弦值．
已知函数f（x）=loga（x2-ax+2）（a＞0且a≠1）在（2，+∞）上为增函数，则实数a的取值范围为
 
．
若集合M={x|x2-3x+2=0}，U={0，1，2，3，4，5}，∁UM=
 
．
教室中用两根细绳悬吊的日光灯管如图所示，若将它绕中轴线扭转60°，灯管将上升
 
厘米．
已知点A（a，6）到直线3x-4y-4=0的距离等于4，则a的值为
 
．
设{an}为等比数列，Sn为前n项和，若Sn=2•3n-1+4t，则t=
 
．
（理）已知z=x+yi，x，y∈R，i是虚数单位．若复数
z
1+i
+i是实数，则|z|的最小值为（　　）
A、0
B、
5
2
C、5
D、
2
若
a
为任一非零向量，
b
为长度为1的向量，下列各式正确的是（　　）
A、|
a
|＞|
b
|
B、
a
∥
b
C、|
a
|＞0
D、|
b
|=±1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网