题目内容
设数列{an}是公差不为零的等差数列,它的前n项和为Sn,且S1、S2、S4成等比数列,则
等于( )
| a3 |
| a1 |
| A、2 | B、3 | C、4 | D、5 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:由题意可得S22=S1•S4,化简可得 d=2a1,代入
化简可得结果.
| a3 |
| a1 |
解答:
解:数列{an}是公差不为0的等差数列,设公差为d,
S1,S2,S4成等比数列,则 S22=S1•S4,
∴( 2a1+d)2=a1•(4a1+6d),化简可得 d=2a1
∴
=
=5.
故选:D.
S1,S2,S4成等比数列,则 S22=S1•S4,
∴( 2a1+d)2=a1•(4a1+6d),化简可得 d=2a1
∴
| a3 |
| a1 |
| a1+2d |
| a1 |
故选:D.
点评:本题主要考查等差数列的通项公式,等差数列的前n项和公式的应用,求出d=2a1,是解题的关键,属于中档题.

练习册系列答案
相关题目
设等边三角形的边长为a,P是△ABC内的任意一点,且P到三边AB、BC、CA的距离分别为d1、d2、d3,则有d1+d2+d3为定值
a,由以上平面图形的特性类比空间图形:设正四面体ABCD的棱长为a,P是正四面体ABCD内任意一点,即到四个面ABC,ABD,ACD,BCD的距离分别为d1、d2、d3、d4,则有d1+d2+d3+d4为定值( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若向量
=(1,-3),|
|=|
|,
•
=0,则|
|=( )
| OA |
| OA |
| OB |
| OA |
| OB |
| AB |
A、2
| ||
B、6
| ||
C、2
| ||
D、
|
若集合M={1,2,4},N={x|x是8的约数},则M与N的关系是( )
| A、M=N | B、N⊆M |
| C、M⊆N | D、M?N |
设命题p:命题“?x∈R,x2+x+1=0”的否定是“?x∈R,x2+x+1≠0”;命题q:“x>2”是“|x-1|>1”的充分不必要条件,则( )
| A、“p或q”为真 |
| B、“p且q”为真 |
| C、p真q假 |
| D、p,q均为假命题 |
若函数f(x)=(a-2)x2+(a-1)x+3是偶函数,则a=( )
| A、0 | B、1 | C、1或2 | D、2 |
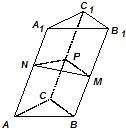 类比正弦定理,如图,在三棱柱ABC-A1B1C1中,二面角B-AA1-C、C-BB1-A、B-CC1-A,所成的平面角分别为α、β、γ,则有
类比正弦定理,如图,在三棱柱ABC-A1B1C1中,二面角B-AA1-C、C-BB1-A、B-CC1-A,所成的平面角分别为α、β、γ,则有


