题目内容

5．某组合体的三视图如图所示，则该几何体的体积为32+8π．

分析 由三视图可知，该几何体是上面长与宽均为4，高为2长方体下接半径为2的半圆柱的组合体，于是可求其体积．

解答 解：依题意知，该几何体是上面长与宽均为4，高为2长方体下接半径为2的半圆柱的组合体，
故其体积为：V=$4×4×2+π×{2^2}×4×\frac{1}{2}=32+8π$．
故答案为：32+8π．

点评 本题考查由三视图求面积、体积，分析出该几何体是上面长与宽均为4，高为2长方体下接半径为2的半圆柱的组合体是关键，考查识图与运算能力，属于中档题．

练习册系列答案
相关题目
18．已知等差数列{an}的前n项和为Sn，且$\frac{{S}_{25}}{{a}_{23}}$=5，$\frac{{S}_{45}}{{a}_{33}}=25$，则$\frac{{S}_{65}}{{a}_{43}}$等于（　　）
A．125B．85C．45D．35
16．设a=0.5${\;}^{\frac{1}{2}}$，b=0.8${\;}^{\frac{1}{2}}$，c=log20.5，则a、b、c的大小关系是（　　）
A．c＜b＜aB．c＜a＜bC．a＜b＜cD．b＜a＜c
13．已知函数f（x）=x|x-2|．
（1）在下列方格中画出f（x）的图象；
（2）写出f（x）的单调区间，并说明函数单调性；（不必证明）
（3）若f（x）=1，求x的值．
20．半径为2，圆心角等于$\frac{2π}{5}$的扇形的面积是$\frac{4π}{5}$．
10．在复平面内，若z=m-3+mi 所对应的点在第二象限，则实数m的取值范围是（　　）
A．（0，3）B．（-∞，-2）C．（-2，0）D．（3，4）
17．方程x2+y2-2x+4y+6=0表示的图形为（　　）
A．一个点B．一个圆C．一条直线D．不存在
14．执行如图所示的程序框图，若输出的i的值为12，则①、②处可填入的条件分别为（　　）
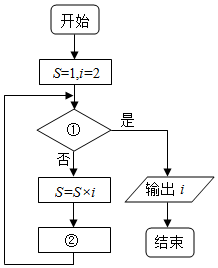
A．S＞384，i=i+1B．S≥384，i=i+2C．S＞3840，i=i+1D．S≥3840，i=i+2
15．若sinα=-$\frac{1}{2}$，cosα=$\frac{\sqrt{3}}{2}$，则角α终边与单位圆交点P的坐标为（$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网