题目内容

13．已知函数f（x）=x|x-2|．
（1）在下列方格中画出f（x）的图象；
（2）写出f（x）的单调区间，并说明函数单调性；（不必证明）
（3）若f（x）=1，求x的值．

分析 （1）作函数f（x）=x|x-2|的图象，从而解得．
（2）结合图象写出函数的单调性；
（3）结合图象可知f（x）=1的一个解为x=1，再解方程x（x-2）=1即可．

解答 解：（1）作函数f（x）=x|x-2|的图象如下，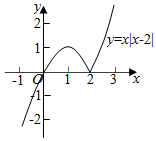

（2）结合图象可知，
f（x）在（-∞，1]，[2，+∞）上单调递增，
在（1，2）上单调递减；
（3）结合图象可知，f（x）=1的一个解为x=1，
由x（x-2）=1解得，
x=1+$\sqrt{2}$，或x=1-$\sqrt{2}$（舍去）；
故x的值为1或1+$\sqrt{2}$．

点评 本题考查了方程的根与函数的零点的关系应用及数形结合的思想应用，属于中档题．

练习册系列答案
相关题目
6．若a＞b＞0，则a2+$\frac{2}{b（a-b）}$的最小值是4$\sqrt{2}$．
4．有5个互不相等的正整数，他们的平均数为9，方差为4，则这组数据中最大的数等于（　　）
A．10B．11C．12D．12
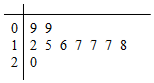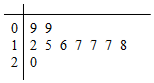1．10名同学参加投篮比赛，每人投20球，投中的次数用茎叶图表示（如图），设其平均数为a，中位数为b，众数为c，则有（　　）
A．a＞b＞cB．b＞c＞aC．c＞a＞bD．c＞b＞a
8．已知函数f（x）=|x2-x|+|x2+$\frac{1}{x}$|（x≠0）．
（1）求证：f（x）≥2；
（2）若?x∈[1，3]，使f（x）≥$\frac{ax+1}{x}$成立，求实数a的取值范围．
18．已知函数$f（x）=2sin（2x-\frac{π}{3}）+1$
（Ⅰ）求f（x）的最小正周期、最值．
（Ⅱ）若对任意的x1，x2∈[0，$\frac{π}{2}$]，都有|f（x1）-f（x2）|＜m，求实数m的取值范围．
5．某组合体的三视图如图所示，则该几何体的体积为32+8π．
2．已知扇形的圆心角为60°，其弧长为2π，则此扇形的面积为6π．
3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$的右焦点为F（1，0），且点P（1，$\frac{3}{2}$）在椭圆C上；
（1）求椭圆C的标准方程；
（2）过椭圆C1：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}-\frac{5}{3}}$=1上异于其顶点的任意一点Q作圆O：x2+y2=$\frac{4}{3}$的两条切线，切点分别为M、N（M、N不在坐标轴上），若直线MN在x轴，y轴上的截距分别为m、n，证明：$\frac{1}{3{m}^{2}}+\frac{1}{{n}^{2}}$为定值；
（3）若P1、P2是椭圆C2：$\frac{{x}^{2}}{{a}^{2}}+\frac{3{y}^{2}}{{b}^{2}}=1$上不同两点，P1P2⊥x轴，圆E过P1、P2，且椭圆C2上任意一点都不在圆E内，则称圆E为该椭圆的一个内切圆，试问：椭圆C2是否存在过焦点F的内切圆？若存在，求出圆心E的坐标；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网