题目内容

10．在复平面内，若z=m-3+mi 所对应的点在第二象限，则实数m的取值范围是（　　）
A．（0，3）B．（-∞，-2）C．（-2，0）D．（3，4）

分析 由z=m-3+mi 所对应的点（m-3，m）在第二象限，则$\left\{\begin{array}{l}{m-3＜0}\\{m＞0}\end{array}\right.$，解出即可得出．

解答 解：若z=m-3+mi 所对应的点（m-3，m）在第二象限，则$\left\{\begin{array}{l}{m-3＜0}\\{m＞0}\end{array}\right.$，解得0＜m＜3．
实数m的取值范围是（0，3），
故选：A．

点评 本题考查了复数的几何意义、坐标性质，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
3．求（1+x2）（x-$\frac{1}{x}$）9的展开式中x5的系数．
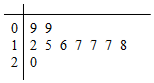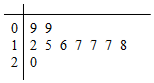1．10名同学参加投篮比赛，每人投20球，投中的次数用茎叶图表示（如图），设其平均数为a，中位数为b，众数为c，则有（　　）
A．a＞b＞cB．b＞c＞aC．c＞a＞bD．c＞b＞a
18．已知函数$f（x）=2sin（2x-\frac{π}{3}）+1$
（Ⅰ）求f（x）的最小正周期、最值．
（Ⅱ）若对任意的x1，x2∈[0，$\frac{π}{2}$]，都有|f（x1）-f（x2）|＜m，求实数m的取值范围．
5．某组合体的三视图如图所示，则该几何体的体积为32+8π．
15．已知一非零向量列{$\overrightarrow{{a}_{n}}$}满足：$\overrightarrow{{a}_{1}}$=（1，$\sqrt{3}$），且$\overrightarrow{{a}_{n}}$=（xn，yn）=$\frac{1}{2}$（xn-1-yn-1，xn-1+yn-1）（n≥2）．
（1）求证：{|$\overrightarrow{{a}_{n}}$|}是等比数列；
（2）求证：$\overrightarrow{{a}_{n-1}}$，$\overrightarrow{{a}_{n}}$（n≥2）的夹角θn为定值．
2．已知扇形的圆心角为60°，其弧长为2π，则此扇形的面积为6π．
19．若曲线y=$\sqrt{|{x}^{2}-4|}$与直线y=x+m恰好有两个交点，则实数m的取值范围是（-2，0）∪{2}∪{$2\sqrt{2}$}．
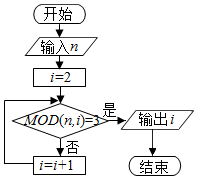20．已知MOD函数是一个求余函数，其格式为MOD（n，m），其结果为n除以m的余数，例如MOD（7，3）=1，如图是一个算法的程序框图，当输入的n值为15时，输出的结果为（　　）
A．4B．5C．6D．7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网