题目内容
如图,在四棱锥 中,
中,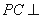 底面ABCD,底面ABCD是直角梯形,
底面ABCD,底面ABCD是直角梯形,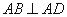 ,
,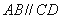 ,
,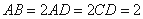 ,E是PB的中点。
,E是PB的中点。
(Ⅰ)求证:平面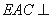 平面PBC;
平面PBC;
(Ⅱ)若二面角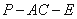 的余弦值为
的余弦值为 ,求直线PA
,求直线PA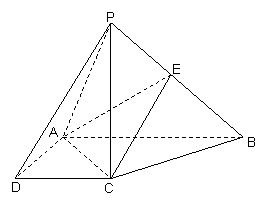 与平面EAC所成角的正弦值。
与平面EAC所成角的正弦值。

(Ⅱ)以C为原点,建立空间直角坐标系如图所示,
则C(0,0,0),A(1,1,0),B(1,-1,0)。
设P(0,0,a)(a>0),则E(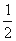 ,
, ,
, ),
),
 ,
, ,
, ,
,

设直线PA与平面EAC所成角为 ,则
,则 ,
,

【思路点拨】(Ⅰ)由已知可得 ,由勾股定理可证出
,由勾股定理可证出 ,所以
,所以 ,再根据面面垂直的判定定理即可得出平面
,再根据面面垂直的判定定理即可得出平面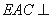 平面PBC;
平面PBC;
(Ⅱ)建立适当的空间直角坐标系,用坐标表示点,进而求出所需向量的坐标,把线面角,二面角转化成对应向量的夹角,利用向量的夹角公式求夹角即可。

练习册系列答案
相关题目
 .
. ,记
,记 ,若
,若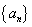 是递减数列,则实数
是递减数列,则实数 的取值范围是______________.
的取值范围是______________. 的一条渐近线与直线2x+y-3=0垂直,则双曲线的离心率是
的一条渐近线与直线2x+y-3=0垂直,则双曲线的离心率是 B.
B. C.
C. D.
D.
 P为 圆上一点,求
P为 圆上一点,求 的最大值。
的最大值。 上定义运算
上定义运算 :
: .若关于
.若关于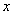 的不等式
的不等式 的解集是集合
的解集是集合 的子集,则实数
的子集,则实数 的取值范围是…………………( ).
的取值范围是…………………( ).







 的分布律如右图,其中
的分布律如右图,其中 成等差数列,如果
成等差数列,如果 ,则
,则 的值等于 )
的值等于 ) B.
B. C.
C. D.
D.







 中,动圆
中,动圆 的半径为1,圆心在线段
的半径为1,圆心在线段 (含端点)上运动,
(含端点)上运动, 是圆
是圆 为实数),则
为实数),则 的最大值为____________.
的最大值为____________.