题目内容
已知直角坐标平面上任意两点P（x1，y1），QP（x2，y2），定义d（P，Q）
为P，Q两点的“非常距离”．当平面上动点M（x，y）到定点A（a，b）的距离满足|MA|=3时，则d（M，A）的取值范围是 ．
|
考点：进行简单的合情推理
专题：新定义,直线与圆
分析：由题意可知点M在以A为圆心，r=3为半径的圆周上，由“非常距离”的新定义，求出d（M，A）的最小值与最大值，即可得出结论．
解答：
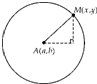解：由题意可知点M在以A为圆心，r=3为半径的圆周上，如图所示：
由“非常距离”的新定义可知：当|x-a|=|y-b|时，d（M，A）取得最小值，d（M，A）min=
；
当|x-a|=3，|y-b|=0或|x-a|=0，|y-b|，=3时，d（M，A）取得最大值，d（M，A）max=3，
故d（M，A）的取值范围为[
，3]．
故答案为：[
，3]．
解：由题意可知点M在以A为圆心，r=3为半径的圆周上，如图所示：由“非常距离”的新定义可知：当|x-a|=|y-b|时，d（M，A）取得最小值，d（M，A）min=
3
| ||
| 2 |
当|x-a|=3，|y-b|=0或|x-a|=0，|y-b|，=3时，d（M，A）取得最大值，d（M，A）max=3，
故d（M，A）的取值范围为[
3
| ||
| 2 |
故答案为：[
3
| ||
| 2 |
点评：本题以新定义为载体，考查数学概念的新定义，数形结合的思想，考查了距离公式的简单应用，属于基础试题．
练习册系列答案
相关题目
下列有关命题的说法正确的是（ ）
| A、命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” |
| B、若p∨q为真命题，则p、q均为真命题． |
| C、命题“存在x∈R，使得x2+x+1＜0”的否定是：“对任意x∈R，均有x2+x+1＜0” |
| D、命题“若x=y，则sinx=siny”的逆否命题为真命题 |
已知集合A={x|2x2+7x-15＜0}，B={x|x2+ax+b≤0}，若A∩B=∅，A∪B={x|-5＜x≤2}，则实数a，b的值分别是（ ）
| A、2，4 | ||
B、
| ||
C、
| ||
D、-
|