题目内容
在△ABC中，内角A、B、C的对边分别是a、b、c，且bsinB=asinA+（c-
a）sinC．
（1）求角B的大小；
（2）设b2-4bcos（A-C）+4=0，求△ABC的面积S．
| 3 |
（1）求角B的大小；
（2）设b2-4bcos（A-C）+4=0，求△ABC的面积S．
考点：正弦定理,余弦定理
专题：解三角形
分析：（1）△ABC中，由条件利用正弦定理可得
ac=a2+c2-b2，再由由余弦定理求得cosB的值，从而求得B的值．
（2）对于b2-4bcos（A-C）+4=0，由判别式△≥0，可得sin2（A-C）=0，进而得A=C，即a=c，且b=2，再由余弦定理求得a2的值，从而求得△ABC的面积S．
| 3 |
（2）对于b2-4bcos（A-C）+4=0，由判别式△≥0，可得sin2（A-C）=0，进而得A=C，即a=c，且b=2，再由余弦定理求得a2的值，从而求得△ABC的面积S．
解答：
解：（1）△ABC中，由bsinB=asinA+（c-
a）sinC利用正弦定理可得b2=a2+(c-
a)c，即
ac=a2+c2-b2．
由余弦定理得cosB=
=
，∴B=30°．
（2）对于b2-4bcos（A-C）+4=0，∵△=16cos2（A-C）-16=-16sin2（A-C）≥0，
∴sin2（A-C）=0，得A=C，且b=
=2．
∴a=c，∴b2=22=2a2-2a2cos30°，
解得a2=
=8+4
，
故S=
a2sin300=2+
．
| 3 |
| 3 |
| 3 |
由余弦定理得cosB=
| a2+c2-b2 |
| 2ac |
| ||
| 2 |
（2）对于b2-4bcos（A-C）+4=0，∵△=16cos2（A-C）-16=-16sin2（A-C）≥0，
∴sin2（A-C）=0，得A=C，且b=
| 4cos(A-C) |
| 2 |
∴a=c，∴b2=22=2a2-2a2cos30°，
解得a2=
| 4 | ||
2-
|
| 3 |
故S=
| 1 |
| 2 |
| 3 |
点评：本题主要考查正弦定理、余弦定理的应用，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
下列命题错误的是（ ）
| A、命题“若x2-3x+2=0，则x=1”的逆否命题为“若x≠1，则x2-3x+2≠0” |
| B、若命题p：?x∈R，x2+x+1=0，则“?p”为：?x∈R，x2+x+1≠0 |
| C、“x＞2”是“x2-3x+2＞0”的充分不必要条件 |
| D、若“p∧q”为假命题，则p，q均为假命题 |
已知集合A={x|
≥0}，集合B={y|y=sinx，x∈R}，则B∩CRA=（ ）
| 1+x |
| 1-x |
| A、∅ | B、{1} |
| C、{-1} | D、{-1，1} |
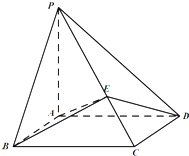如图，在四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD为平行四边形，AB=1，BC=
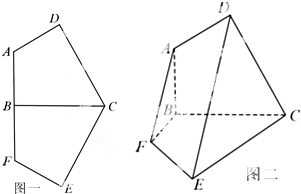已知轴对称平面五边形ADCEF（如图1），BC为对称轴，AD⊥CD，AD=AB=1，CD=BC=