题目内容
求适合下列条件的圆锥曲线标准方程:
(1)过点(-3,2)且与
+
=1有相同焦点的椭圆的标准方程;
(2)以原点为顶点,坐标轴为对称轴,并且经过点P(-4,-4
)的抛物线的标准方程.
(1)过点(-3,2)且与
| x2 |
| 9 |
| y2 |
| 4 |
(2)以原点为顶点,坐标轴为对称轴,并且经过点P(-4,-4
| 2 |
考点:椭圆的简单性质,抛物线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设椭圆方程为
+
=1,代入点(-3,2),可得椭圆的标准方程;
(2)分类设出抛物线的方程,代入P(-4,-4
),可得结论.
| x2 |
| 9+λ |
| y2 |
| 4+λ |
(2)分类设出抛物线的方程,代入P(-4,-4
| 2 |
解答:
解:(1)设椭圆方程为
+
=1,
代入点(-3,2),可得
+
=1,
∴λ=6,
∴所求方程为
+
=1;
(2)设抛物线方程为x2=-2py,代入P(-4,-4
),可得p=
,∴抛物线方程为x2=-2
y;
设抛物线方程为y2=-2p′x,代入P(-4,-4
),可得p′=4,∴抛物线方程为y2=-8y.
| x2 |
| 9+λ |
| y2 |
| 4+λ |
代入点(-3,2),可得
| 9 |
| 9+λ |
| 4 |
| 4+λ |
∴λ=6,
∴所求方程为
| x2 |
| 15 |
| y2 |
| 10 |
(2)设抛物线方程为x2=-2py,代入P(-4,-4
| 2 |
| 2 |
| 2 |
设抛物线方程为y2=-2p′x,代入P(-4,-4
| 2 |
点评:解决此类题目的关键方是掌握椭圆、抛物线中相关的数值,灵活运用待定系数法求标准方程.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
一批产品分为一、二、三级,其中一级品是二级品的2倍,三级品为二级品的一半,从这批产品中随机抽取一个检验,其级别为随机变量ξ,则Eξ的值为( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
 已知一个正四面体纸盒的俯视图如图所示,其中四边形ABCD是边长为3
已知一个正四面体纸盒的俯视图如图所示,其中四边形ABCD是边长为3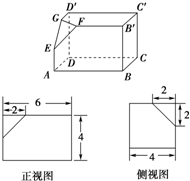 如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).
如图所示的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm).