题目内容
在约束条件
下，则目标函数z=4x+2y的取值范围是（ ）
|
| A、[0，12] |
| B、[2，10] |
| C、[0，10] |
| D、[2，12] |
考点：简单线性规划
专题：数形结合法
分析：先作出不等式组表示的平面区域，结合图象及z的几何意义可求z的范围．
解答：
解：约束条件
下，可行域如图所示，A（0，1），B（2，1），
由图知，目标函数z=4x+2y过点A（0，1）时，有最小值2，
目标函数z=4x+2y过点B（2，1）时，有最大值10，
故选：B．
解：约束条件
|
由图知，目标函数z=4x+2y过点A（0，1）时，有最小值2，
目标函数z=4x+2y过点B（2，1）时，有最大值10，
故选：B．
点评：本题在主要考查了线性规划的基本应用，属于基础试题
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
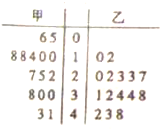从甲乙两个城市分别随机抽取15台自动售货机，对其销售额进行统计，统计数据用茎叶图表示（如图所示），设甲乙两组数据的平均数分别为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线
-
=1（a＞0，b＞0）的右焦点与抛物线y2=12x的焦点重合，且双曲线的一条渐近线被圆（x-3）2+y2=8截得的弦长为4，则此双曲线的渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、y=±2x | ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±2
|
一个样本容量为20的样本数据，它们组成一个等差数列{an}，若a1=4，a20=42，则此样本的平均数和中位数分别是（ ）
| A、22，23 |
| B、23，22 |
| C、23，24 |
| D、23，23 |
一批产品分为一、二、三级，其中一级品是二级品的2倍，三级品为二级品的一半，从这批产品中随机抽取一个检验，其级别为随机变量ξ，则Eξ的值为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、2 |
已知数列{an}是等差数列，a1+a3+a5=105，a2+a4+a6=99，{an}的前n项和为Sn，则使得Sn达到最大的n是（ ）
| A、18 | B、19 | C、20 | D、21 |
设∠A，∠B，∠C是△ABC的三个内角，且tanA、
、tanB成等差数列，tanA、
、tanB成等比数列，则△ABC是（ ）
| 5 |
| 12 |
| ||
| 6 |
| A、锐角三角形 |
| B、等边三角形 |
| C、钝角三角形 |
| D、等腰直角三角形 |