题目内容
设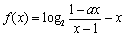 为奇函数,
为奇函数,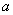 为常数.
为常数.
(1)求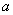 的值;
的值;
(2)判断并证明函数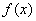 在
在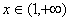 时的单调性;
时的单调性;
(3)若对于区间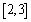 上的每一个
上的每一个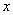 值,不等式
值,不等式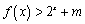 恒成立,求实数
恒成立,求实数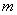 取值范围.
取值范围.
解:(1)由条件得: ,
, ,
,
化简得 ,
,
因此 ,但
,但 不符合题意,因此
不符合题意,因此 .
.
(也可以直接根据函数定义域关于坐标原点对称,得出结果,同样给分)
(2)判断函数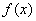 在
在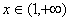 上为单调减函数;
上为单调减函数;
证明如下:设







又 

 ,
, ,又
,又

 ,即
,即
 函数
函数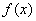 在
在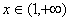 上为单调减函数;
上为单调减函数;
(也可以利用导数证明,对照给分)
(3)不等式为 恒成立,
恒成立,
 在
在
 上单调递减,
上单调递减, 在
在 上单调递增,
上单调递增,
 在
在
 上单调递减,
上单调递减,
当 时取得最小值为
时取得最小值为 ,
, 。
。

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 为双曲线
为双曲线 虚轴的一个端点,
虚轴的一个端点, 为双曲线上的一个动点,则
为双曲线上的一个动点,则 的最小值为 .
的最小值为 .
 .
. ,则
,则 的大小关系为 .
的大小关系为 . ,设锥形容器的高为
,设锥形容器的高为 ,顶口直径为
,顶口直径为 ,求当水深为
,求当水深为 时,水面上升的速度.
时,水面上升的速度.
 的终边过点
的终边过点 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
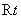 △
△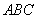 直角边
直角边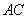 上一点
上一点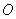 为圆心
为圆心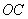 为半径的⊙
为半径的⊙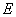 ,
,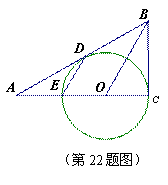
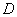 为斜边
为斜边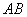 上一点,且OD=OC,
上一点,且OD=OC,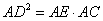 .
.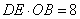 ,求⊙
,求⊙ 在区间
在区间 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列 .(Ⅰ)求数列
.(Ⅰ)求数列 的通项公式;
的通项公式; ,数列
,数列 的前
的前 项和为
项和为 ,求
,求