题目内容

已知sin（
3π
2
+α）=
1
3
，求cos（π-α）的值．
考点：运用诱导公式化简求值,同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知等式利用诱导公式化简求出cosα的值，原式利用诱导公式化简，把cosα的值代入计算即可求出值．
解答： 解：∵sin（
3π
2
+α）=-cosα=
1
3
，
∴cosα=-
1
3
，
则原式=-cosα=
1
3
．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
△ABC的内角A，B，C所对的边分别是a，b，c．若B=105°，C=15°，则
2a
bcos15°+ccos105°
的值为
 
．
设集合A=[0，1），B=[1，2]，函数f（x）=
2x，(x∈A)
4-2x，(x∈B)
，x0∈A，且f[f（x0）]∈A，则x0 的取值范围是（　　）
A、（
2
3
，1）
B、[0，
3
4
]
C、（log2
3
2
，1）
D、（log32，1）
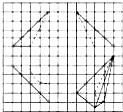如图，网格纸上小正方形的边长为1，粗线或粗虚线画出了某简单组合体的三视图和直观图（斜二测画法），则此简单几何体的体积是
 
．
已知cos（α-
π
4
）=
1
2
，求sin2α的值．
在实数集R内，我们用“＜”为全体实数排了一个“序”，类似的，我们在向量集上也可以定义一个“序”的关系，记为“?”，定义如下：对于任意两个向量
m1
=（x1，y1）•（x1，y1∈R），
m2
=（x2，y2）•（x2，y2∈R），当取仅当“x1＜x2“或“x1=x2且y1＜y2∈R”时，
m1
?
m2
，按上述定义的关系“?”，给出如下四个命题：
①若
m1
?
m2
，则|
m1
|≤|
m2
|；
②若
m1
?
m2
，
m2
?
m3
，则，则
m1
?
m3
；
③若
m1
?
m2
，则对于任意
m
，都有（
m1
+
m
）?（
m2
+
m
）成立；
④对于实数λ≥0，若
m1
?
m2
，则λ
m1
?λ
m2
成立；
其中所有命题的个数为（　　）
A、1B、2C、3D、4
定义运算a*b，a*b
a，a≤b
b，a＞b
，例如1*2=1，已知函数f（x）=1*ax（0＜a＜1）且f（4）=
1
2014
，则f（2）=（　　）
A、-1007
B、-1006
C、1007
D、
1
2014
如图（1），在边长为2的正方形ABCD中，E是边AB的中点．将△ADE沿DE折起使得平面ADE⊥平面BCDE，如图（2），F是折叠后AC的中点．

（Ⅰ）求证：BF∥平面ADE；
（Ⅱ）求二面角E-AB-D的平面角的余弦值．
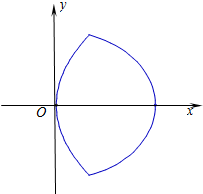如图，曲线E是由抛物线弧E1：y2=4x（0≤x≤
2
3
）与椭圆弧E2：
x2
a2
+
y2
b2
=1（
2
3
≤x≤a）所围成的封闭曲线，且E1与E2有相同的焦点．
（Ⅰ）求椭圆弧E2的方程；
（Ⅱ）设过点F（1，0）的直线与曲线E交于A，B两点，|FA|=r1，|FB|=r2，且∠AFx=α（0≤α≤π），试用cosα表示r1；并求
r1
r2
的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网