题目内容
已知函数f(x)=xlnx(x∈(0,+∞)).
(1)求f(x)的单调区间;
(2)若函数g(x)=2f(x)-blnx+x在x∈[1,+∞)上存在零点,求实数b的取值范围.
(1)求f(x)的单调区间;
(2)若函数g(x)=2f(x)-blnx+x在x∈[1,+∞)上存在零点,求实数b的取值范围.
考点:利用导数研究函数的极值
专题:计算题,存在型,导数的综合应用
分析:求导后可知单调区间;通过独立参数,构造函数,转化为最值问题.
解答:
解:(1)f(x)=xlnx,f'(x)=lnx+1;
令f'(x)>0,即:lnx+1>0,
解得:x>
,即f(x)在(
,+∞)上单调递增;
令f'(x)<0,即:lnx+1<0
解得:0<x<
,即f(x)在(0,
)上单调递减.
综上所述,f(x)的单调增区间是:(
,+∞),单调减区间是:(0,
).
(2)∵函数g(x)=2f (x)-blnx+x在[1,+∞)上存在零点,
∴方程2xlnx-blnx+x=0在[1,+∞)上有实数解.
易知x=1不是方程的实数解,
∴方程2xlnx-blnx+x=0在(1,+∞)上有实数解,
即方程b=2x+
在(1,+∞)上有实数解.
设g(x)=2x+
(x>1),
g′(x)=2+
=
,
∵x>1,
∴lnx>0,lnx+1>0,
当2lnx-1>0,即x>
时,g′(x)>0,
当2lnx-1<0,即1<x<
时,g′(x)<0,
∴g(x)在(1,
)上单调递减,在(
,+∞)上单调递增,
∴g(x)min=4
,
∴实数b的取值范围为[4
,+∞).
令f'(x)>0,即:lnx+1>0,
解得:x>
| 1 |
| e |
| 1 |
| e |
令f'(x)<0,即:lnx+1<0
解得:0<x<
| 1 |
| e |
| 1 |
| e |
综上所述,f(x)的单调增区间是:(
| 1 |
| e |
| 1 |
| e |
(2)∵函数g(x)=2f (x)-blnx+x在[1,+∞)上存在零点,
∴方程2xlnx-blnx+x=0在[1,+∞)上有实数解.
易知x=1不是方程的实数解,
∴方程2xlnx-blnx+x=0在(1,+∞)上有实数解,
即方程b=2x+
| x |
| lnx |
设g(x)=2x+
| x |
| lnx |
g′(x)=2+
| lnx-1 |
| (lnx)2 |
| (2lnx-1)(lnx+1) |
| (lnx)2 |
∵x>1,
∴lnx>0,lnx+1>0,
当2lnx-1>0,即x>
| e |
当2lnx-1<0,即1<x<
| e |
∴g(x)在(1,
| e |
| e |
∴g(x)min=4
| e |
∴实数b的取值范围为[4
| e |
点评:本题综合考查了导数的应用,同时考查了函数与方程之间的关系及数形结合的思想,属于中档题.

练习册系列答案
相关题目
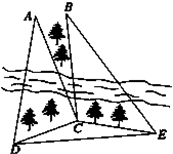 如图,某测量人员为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1百米.
如图,某测量人员为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1百米.