题目内容
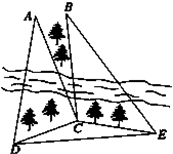 如图,某测量人员为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1百米.
如图,某测量人员为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1百米.(1)求△CDE的面积;
(2)求A,B之间的距离的平方.
考点:正弦定理,两角和与差的余弦函数
专题:解三角形
分析:(1)利用周角定义求出∠DCE度数,再由CD与CE的长,利用三角形面积公式求出三角形CDE面积即可;
(2)连接AB,在直角三角形ACD中,利用锐角三角函数定义求出AC的长,在直角三角形BCE中,求出∠CBE度数,利用正弦定理求出BC的长,在三角形ABC中,利用余弦定理求出AB的平方即可.
(2)连接AB,在直角三角形ACD中,利用锐角三角函数定义求出AC的长,在直角三角形BCE中,求出∠CBE度数,利用正弦定理求出BC的长,在三角形ABC中,利用余弦定理求出AB的平方即可.
解答:
 解:(1)在△CDE中,∠DCE=360°-90°-15°-105°=150°,
解:(1)在△CDE中,∠DCE=360°-90°-15°-105°=150°,
∴S△CDE=
CD•CE•sin150°=
×1×1×
=
(平方百米);
(2)连接AB,
根据题意知,在Rt△ACD中,AC=DC•tan∠ADC=1×tan60°=
(百米),
在△BCE中,∠CBE=180°-∠BCE-∠CEB=180°-105°-45°=30°,
由正弦定理
=
得:BC=
=
=
(百米),
∵cos15°=cos(60°-45°)=cos60°cos45°+sin60°sin45°=
,
在△ABC中,由余弦定理得:AB2=AC2+BC2-2AC•BCcos∠ACB,
则AB2=3+2-2
×
×
=2-
(百米).
 解:(1)在△CDE中,∠DCE=360°-90°-15°-105°=150°,
解:(1)在△CDE中,∠DCE=360°-90°-15°-105°=150°,∴S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)连接AB,
根据题意知,在Rt△ACD中,AC=DC•tan∠ADC=1×tan60°=
| 3 |
在△BCE中,∠CBE=180°-∠BCE-∠CEB=180°-105°-45°=30°,
由正弦定理
| BC |
| sin∠CEB |
| CE |
| sin∠CBE |
| CE•sin∠CEB |
| sin∠CBE |
1×
| ||||
|
| 2 |
∵cos15°=cos(60°-45°)=cos60°cos45°+sin60°sin45°=
| ||||
| 4 |
在△ABC中,由余弦定理得:AB2=AC2+BC2-2AC•BCcos∠ACB,
则AB2=3+2-2
| 3 |
| 2 |
| ||||
| 4 |
| 3 |
点评:此题考查了正弦、余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
 如图,椭圆C1:
如图,椭圆C1: 将正奇数组成的数列{an}的项:1,3,5,7,9,11,…,按下表排成5列:
将正奇数组成的数列{an}的项:1,3,5,7,9,11,…,按下表排成5列: