题目内容

设A，B为两个不相等的集合，条件p：x∉（A∩B），条件q：x∉（A∪B），则p是q的（　　）
A、充分不必要条件
B、充要条件
C、必要不充分条件
D、既不充分也不必要条件
考点：必要条件、充分条件与充要条件的判断
专题：集合,简易逻辑
分析：根据集合关系，以及充分条件和必要条件的定义进行判断即可．
解答： 解：当x∈A，且x∉（A∩B），满足x∈（A∪B），即充分性不成立，
若x∉（A∪B，则x∉（A∩B），成立，即必要性成立，
故p是q必要不充分条件，
故选：C
点评：本题主要考查充分条件和必要条件的判断，根据集合关系是解决本题的关键．
练习册系列答案
相关题目
小强参加一次测试，共有三道必答题，他是否答对每题互不影响．已知他只答对第一题的概率为0.08，只答对第一题和第二题的概率为0.1，至少答对一题的概率为0.88，用X表示小强答对题的数目．
（Ⅰ）求小强答对第一题的概率；
（Ⅱ）求X的分布列和数学期望．
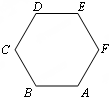
如图，正六边形ABCDEF中，边长为1，|
BA
+
CD
-
EF
|=（　　）
A、1
B、
3
C、2
D、3
已知函数f（x）=
1-x2
若0＜x1＜x2＜1，则（　　）
A、
f(x1)
x1
＞
f(x2)
x2
B、
f(x1)
x1
=
f(x2)
x2
C、
f(x1)
x1
＜
f(x2)
x2
D、前三个判断都不正确
“θ=-
π
3
”是“tanθ=2cos（
π
2
-θ）”的
 
条件．
判断下列命题的真假：
（1）如果一个幂函数不是偶函数，那么它一定是奇函数；
（2）幂函数的图象不可能在第四象限；
（3）幂函数的图象与坐标轴最多只有一个交点；
（4）当a=0时，函数y=xa的图象是一条直线；
（5）若f（x）=x4是奇函数，则他在定义域内单调递增；
（6）如果一个幂函数是奇函数，则它的图象一定经过原点；
（7）任何两个幂函数的图象最多有三个交点；
（8）指数函数图象都经过（0，1）点；
（9）指数函数y=ax（a＞0且a≠1）中，若a＞1，则x＜0时，y＞1；
（10）指数函数y=4x与y=-4x关于y轴对称；
（11）函数f（x）=
1
2x+1
在（-∞，+∞）上单调递减无最大值；
（12）若0＜a＜1，b＜-1，则函数f（x）=ax+b的图象不经过第一象限．
某游泳馆每天的固定成本为500元，门票每张30元，变动成本与购票进入的人数的算术平方根成正比．一天购票人数为25人时，该馆收支平衡；一天购票人数超过100人时，该馆需增加管理费200元．设每天的购票人数为x人，盈利额为y元．
（1）求y与x之间的函数关系；
（2）该馆希望在人数达到20人时就不出现亏损，若用提高门票价格的措施，则每张门票至少要提高多少元（取整数）？
（参考数据：
2
≈1.41，
3
≈1.73，
5
≈2.24）
已知命题p：“方程x2-ax+a+3=0有解”，q：“
1
4x
+
1
2x
-a＞0在[1，+∞）上恒成立”，若p或q为真命题，p且q为假命题，求实数a的取值范围．
已知向量
a
=（cos（-θ），sin（π+θ）），
b
=（cos（
π
2
-θ），sin（
π
2
-θ））．
（Ⅰ）求证
a
⊥
b
；
（Ⅱ）若存在不等于0的实数k和t，使
x
=
a
+（t2+3）
b
，
y
=-k
a
+t
b
满足
x
⊥
y
，试求此时
k+t2
t
的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网