题目内容
20.给出下列四个命题:①若x∈A∩B,则x∈A或x∈B;
②?x∈(2+∞),都有x2>2x;
③若a,b是实数,则a>b是a2>b2的充分不必要条件;
④“?x0∈R,x02+2>3x0”的否定是“?x∈R,x2+2≤3x”;
其中真命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由元素与集合间的关系判断①;举例说明②③错误;真直接写出特称命题的否定判断④.
解答 解:①若x∈A∩B,则x∈A且x∈B,故①错误;
②当x=4时,x2=2x,故命题?x∈(2+∞),都有x2>2x错误;
③当a=2,b=-4时,满足a>b,此时a2<b2,则a>b是a2>b2的不充分条件,故③错误;
④“?x0∈R,x02+2>3x0”的否定是“?x∈R,x2+2≤3x”,故④正确.
∴其中真命题的个数是1个.
故选:A.
点评 本题考查命题的真假判断与应用,考查充分必要条件的判定方法,考查命题的否定,是基础题.

练习册系列答案
相关题目
8. 某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )
某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )
 某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )
某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )| A. | 14,9.5 | B. | 9,9 | C. | 9,10 | D. | 14,9 |
15.已知向量$\overrightarrow{a}$=(m,2),$\overrightarrow{b}$=(2,-1),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\frac{|2\overrightarrow{a}-\overrightarrow{b}|}{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}$等于( )
| A. | $-\frac{5}{3}$ | B. | 1 | C. | 2 | D. | $\frac{5}{4}$ |
12.已知复数z=(2+i)(a+2i3)在复平面内对应的点在第四象限,则实数a的取值范围是( )
| A. | (-∞,-1) | B. | (4,+∞) | C. | (-1,4) | D. | (-4,-1) |
9.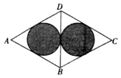 如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )
如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )
 如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )
如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )| A. | $\frac{\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{18π}$ | C. | $\frac{\sqrt{3}π}{18}$ | D. | $\frac{\sqrt{3}π}{9}$ |
10.若x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y≤0\\ y≥0\end{array}\right.$,则x+2y的最大值为( )
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 2 |
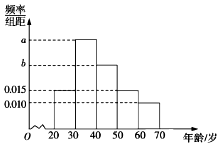 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.