题目内容
19.已知在锐角△ABC中,角A,B,C的对边分别是a,b,c,2asinB=$\sqrt{3}$b,b=2,c=3,AD是角A的平分线,D在BC上,则BD=$\frac{{3\sqrt{7}}}{5}$.分析 由已知及正弦定理可得$2sinAsinB=\sqrt{3}sinB$,结合sinB≠0,可得sinA=$\frac{\sqrt{3}}{2}$,可求A的值,由余弦定理可得a,根据角分线定理可求BD的值.
解答 解:∵2asinB=$\sqrt{3}$b,
∴由正弦定理可得$2sinAsinB=\sqrt{3}sinB$,
∵sinB≠0,可得sinA=$\frac{\sqrt{3}}{2}$,
∴由A为锐角,可得$A=\frac{π}{3}$,
∵b=2,c=3,
∴由余弦定理可得a2=b2+c2-2bcosA=4+9-2×$2×3×\frac{1}{2}$=7,可得:a=$BC=\sqrt{7}$,
∴根据角分线定理可知,$BD=\frac{{3\sqrt{7}}}{5}$.
故答案为:$\frac{{3\sqrt{7}}}{5}$.
点评 本题主要考查了正弦定理,余弦定理,角分线定理在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
相关题目
7.已知$α∈R,sinα+2cosα=\frac{{\sqrt{10}}}{2}$,则tan2α=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
8. 某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )
某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )
 某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )
某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是( )| A. | 14,9.5 | B. | 9,9 | C. | 9,10 | D. | 14,9 |
9.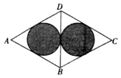 如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )
如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )
 如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )
如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )| A. | $\frac{\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{18π}$ | C. | $\frac{\sqrt{3}π}{18}$ | D. | $\frac{\sqrt{3}π}{9}$ |
 如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.
如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.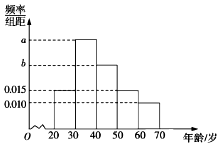 根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.
根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示.