题目内容
12.已知函数f(x)=cos2x+cos2x,求(1)周期;
(2)当x∈[$\frac{π}{6}$,$\frac{2π}{3}$],求值域.
分析 (1)求出f(x)=$\frac{3}{2}$cos2x+$\frac{1}{2}$,从而求出周期T的值;(2)根据x的范围,求出f(x)的值域即可.
解答 解:(1)f(x)=cos2x+cos2x
=cos2x+$\frac{1+cos2x}{2}$
=$\frac{3}{2}$cos2x+$\frac{1}{2}$,
∴T=$\frac{2π}{2}$=π;
(2)x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,2x∈[$\frac{π}{3}$,$\frac{4π}{3}$],
显然2x=π,f(x)最小,最小值是-1,
2x=$\frac{π}{3}$或$\frac{4π}{3}$时,f(x)最大,最大值是$\frac{5}{4}$,
故f(x)的值域是[-1,$\frac{5}{4}$].
点评 本题考查了求函数的周期问题,考查函数的值域问题,熟练掌握三角函数的性质是解题的关键,本题是一道基础题.

练习册系列答案
相关题目
17.在△ABC中,设D为BC的中点,则3$\overrightarrow{AB}$+2$\overrightarrow{BC}$+$\overrightarrow{CA}$=( )
| A. | $\overrightarrow{AD}$ | B. | 2$\overrightarrow{AD}$ | C. | 3$\overrightarrow{AD}$ | D. | 4$\overrightarrow{AD}$ |
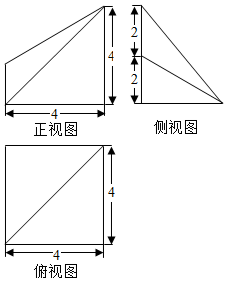 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{80}{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{80}{3}$.