题目内容

设△ABC的内角A，B，C的对边分别为a，b，c，且∠A=60°，2a=3b，则
c
b
的值为
 
．
考点：余弦定理,正弦定理
专题：解三角形
分析：由余弦定理可得：a2=b2+c2-2bccosA，又a=
3b
2
，代入化简即可得出．
解答： 解：由余弦定理可得：a2=b2+c2-2bccosA，又a=
3b
2
，
∴
9b2
4
=b2+c2-2bccos60°，
化为4(
c
b
)2-4×
c
b
-5=0，
解得
c
b
=
1+
6
2
．
故答案为：
1+
6
2
．
点评：本题考查了余弦定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
设曲线C：f（x）=lnx-ax（a∈R），f′（x）表示f（x）导函数．
（Ⅰ）讨论函数f（x）的极值；
（Ⅱ）函数f（x）是否存在两个零点m，n（m＜n），若存在，求实数a的取值范围；
（Ⅲ）对于曲线C上的不同两点A（x1，y1），B（x2，y2），x1＜x2，求证：存在唯一的x0∈（x1，x2），使直线AB的斜率等于f′（x0）．
已知二次函数f（x）有两个零点0和-2，且它有最小值-1．
（1）求f（x）解析式；
（2）若g（x）与f（x）图象关于原点对称，求g（x）解析式．
在△ABC中，C=2A，cosA=
3
4
，则
c
a
=
 
．
组合式
C
0
n
-2
C
1
n
+4
C
2
n
-8
C
3
n
+…+（-2）n
C
n
n
的值等于（　　）
A、（-1）n
B、1
C、3n
D、3n-1
数列{an}的前n项和Sn=n2-2n-1，则a3+a17=（　　）
A、15B、17C、34D、398
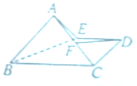如图 所示的几何体ABCDE中，底面BCDE是∠C，∠D为直角的直角梯形，侧面ABE是∠A为直角的直角三角形，且AB=CD=6，BC=6
2
，AE=DE=3
2
；若二面角A-BE-C为直二面角，且F为AC的中点，求证：
（1）FD∥平面ABE；
（2）AC⊥BE．
数列{an}的通项公式为an=6n-3，数列{bn}的通项公式为bn=5n-4，若an≤1000．bn≤1000，由数列{an}与数列{bn}中共有的项构成数列{cn}，则数列{cn}中共有
 
项．
函数f（x）=mx+1-m在区间[0，1]上无零点，则m的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网