题目内容
若-
<θ<-π,那么(tanθ,cosθ)在 象限?
| 3π |
| 2 |
考点:三角函数值的符号
专题:三角函数的求值
分析:判断角所在象限,通过三角函数的符号,判断点所在象限即可.
解答:
解:-
<θ<-π,是第二象限角,
tanθ<0,cosθ<0,
(tanθ,cosθ)在第三象限.
故答案为:三.
| 3π |
| 2 |
tanθ<0,cosθ<0,
(tanθ,cosθ)在第三象限.
故答案为:三.
点评:本题考查三角函数的符号判断,注意角的范围是解题的关键.

练习册系列答案
相关题目
组合式
-2
+4
-8
+…+(-2)n
的值等于( )
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| A、(-1)n |
| B、1 |
| C、3n |
| D、3n-1 |
定义在实数集R上的函数y=f(x)的图象是连续不断的,若对任意的实数x,存在不为0的常数r使得f(x+r)=-rf(x)恒成立,则称f(x)是一个“关于r函数”,下列“关于r函数”的结论正确的是( )
| A、f(x)=0是常数函数中唯一一个“关于r函数” | ||
| B、f(x)=x2是一个“关于r函数” | ||
| C、f(x)=sinπx不是一个“关于r函数” | ||
D、“关于
|
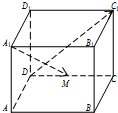 如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,M是棱CD的中点,则
如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,M是棱CD的中点,则| A1M |
| DC1 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
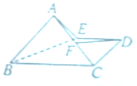 如图 所示的几何体ABCDE中,底面BCDE是∠C,∠D为直角的直角梯形,侧面ABE是∠A为直角的直角三角形,且AB=CD=6,BC=6
如图 所示的几何体ABCDE中,底面BCDE是∠C,∠D为直角的直角梯形,侧面ABE是∠A为直角的直角三角形,且AB=CD=6,BC=6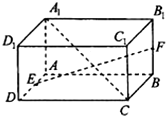 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,点E、F分别是AD、BB1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=AA1=2,点E、F分别是AD、BB1的中点.