题目内容
直三棱柱ABC-EFG所有顶点在半径为
的球面上,AB=AC=
,AE=2,B-AE-C余弦为( )
| 2 |
| 3 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点:二面角的平面角及求法
专题:空间位置关系与距离
分析:根据条件求出AE=BE=CE=1,根据二面角的定义求出二面角的平面角,即可得到结论
解答:
解:如图
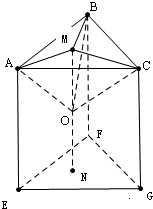
∵直三棱柱ABC-EFG的所有顶点都在半径为
的球面上,
∴球心O位于高的中点上,
∵AE=2,AO=
,
∴OM=1,AM=
=1,
同理MC=MB=1,即O在平面ABC的射影M为三角形ABC的外心,
∵AB=AC=
,
∴cosBAM=
=
=
,
则∠BAM=
,同理∠CAM=
,
则∠BAC=
,
则∠BAC是二面角B-AE-C的平面角,
则cos∠BAC=cos
=
;
故选D.

∵直三棱柱ABC-EFG的所有顶点都在半径为
| 2 |
∴球心O位于高的中点上,
∵AE=2,AO=
| 2 |
∴OM=1,AM=
| OA2-OM2 |
同理MC=MB=1,即O在平面ABC的射影M为三角形ABC的外心,
∵AB=AC=
| 3 |
∴cosBAM=
| AB2+AM2-BM2 |
| 2AB×AM |
| 3+1-1 | ||
2
|
| ||
| 2 |
则∠BAM=
| π |
| 6 |
| π |
| 6 |
则∠BAC=
| π |
| 3 |
则∠BAC是二面角B-AE-C的平面角,
则cos∠BAC=cos
| π |
| 3 |
| 1 |
| 2 |
故选D.
点评:本题主要考查三棱柱中二面角的求法,首先根据二面角的定义找出二面角的平面角,然后计算大小,属于中档题.

练习册系列答案
相关题目
如果椭圆4x2+y2=k上两点间的最大距离是8,那么k等于( )
| A、32 | B、16 | C、8 | D、4 |
以边长为1的正方形的一条边为旋转轴,旋转一周后所得旋转体侧面积为( )
| A、2π | B、π | C、2 | D、1 |
 如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥底面ABCD,SA=AB=2,AD=1,∠ABC=60°,E在棱SD上.
如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,SA⊥底面ABCD,SA=AB=2,AD=1,∠ABC=60°,E在棱SD上. 如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点. 如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是
如图,直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,点E,F分别是