题目内容
14.(1)计算$\frac{1-i}{{{{(1+i)}^2}}}+\frac{1+i}{{{{(1-i)}^2}}}$(2)求中心在原点,焦点在坐标轴上,并且经过点P(3,$\frac{15}{4}$)和Q($\frac{16}{3}$,5)的双曲线方程.
分析 (1)直接利用复数代数形式的乘除运算化简得答案;
(2)由题意设出双曲线方程为$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{n}=1$,代入两点的坐标,联立方程组求得m,n的值得答案.
解答 解:(1)$\frac{1-i}{{{{(1+i)}^2}}}+\frac{1+i}{{{{(1-i)}^2}}}$=$\frac{1-i}{2i}+\frac{1+i}{-2i}$=$\frac{(1-i)(-i)}{-2{i}^{2}}+\frac{(1+i)i}{-2{i}^{2}}=\frac{-1-i-1+i}{2}=-1$;
(2)由题意设双曲线方程为$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{n}=1$,
∵双曲线经过点P(3,$\frac{15}{4}$)和Q($\frac{16}{3}$,5),
∴$\left\{\begin{array}{l}{\frac{9}{m}-\frac{225}{16n}=1}\\{\frac{256}{9m}-\frac{25}{n}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-16}\\{n=-9}\end{array}\right.$.
∴双曲线方程为:$\frac{y^2}{9}-\frac{x^2}{16}=1$.
点评 本题考查复数代数形式的乘除运算,考查双曲线方程的求法,是基础题.

练习册系列答案
相关题目
5.已知圆(x+a)2+y2=4截直线x-y-4=0所得的弦的长度为$2\sqrt{2}$,则a等于( )
| A. | $±2\sqrt{2}$ | B. | 6 | C. | 2或6 | D. | -2或-6 |
2.曲线的参数方程为$\left\{\begin{array}{l}x=1+2cosθ\\ y=2+3sinθ\end{array}\right.(θ为参数)$,则该曲线的普通方程为( )
| A. | $\frac{{{{(x+1)}^2}}}{4}-\frac{{{{(y+2)}^2}}}{9}=1$ | B. | $\frac{{{{(x-1)}^2}}}{4}-\frac{{{{(y-2)}^2}}}{9}=1$ | C. | $\frac{{{{(x+1)}^2}}}{4}+\frac{{{{(y+2)}^2}}}{9}=1$ | D. | $\frac{{{{(x-1)}^2}}}{4}+\frac{{{{(y-2)}^2}}}{9}=1$ |
19.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,它是形成雾霾天气的主要原因之一.PM2.5日均值越小,空气质量越好.2012年2月29日,国家环保部发布的《环境空气质量标准》见表:
针对日趋严重的雾霾情况各地环保部门做了积极的治理.马鞍山市环保局从市区2015年11月~12月和2016年11月~12月的PM2.5检测数据中各随机抽取15天的数据来分析治理效果.样本数据如茎叶图所示(十位为茎,个位为叶)
(Ⅰ)分别求这两年样本数据的中位数和平均值,并以此推断2016年11月~12月的空气质量是否比2015年同期有所提高?
(Ⅱ)在2016年的样本数据中随机抽取3天,以X表示抽到空气质量为一级的天数,求X的分布列与期望.
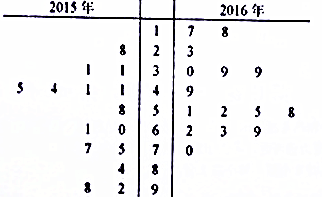
针对日趋严重的雾霾情况各地环保部门做了积极的治理.马鞍山市环保局从市区2015年11月~12月和2016年11月~12月的PM2.5检测数据中各随机抽取15天的数据来分析治理效果.样本数据如茎叶图所示(十位为茎,个位为叶)
| PM2.5日均值k(微克) | 空气质量等级 |
| k≤35 | 一级 |
| 35<k<75 | 二级 |
| k>75 | 超标 |
(Ⅱ)在2016年的样本数据中随机抽取3天,以X表示抽到空气质量为一级的天数,求X的分布列与期望.
