题目内容
已知f(x)的定义域是[0,4],则f(x+1)+f(x-1)的定义域 ;f(x+1)的定义域是[0,4],则f(2x-1)的定义域为 .
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:(1)由题意得不等式组,解出即可;(2)先求出1≤x+1≤5,得到函数f(x)的定义域,从而1≤2x-1≤5,解出即可.
解答:
解:(1)由题意得:
,解得:1≤x≤3;
(2)∵0≤x≤4,∴1≤x+1≤5,
∴1≤2x-1≤5,解得:1≤x≤3;
故答案为:[1,3],[1,3].
|
(2)∵0≤x≤4,∴1≤x+1≤5,
∴1≤2x-1≤5,解得:1≤x≤3;
故答案为:[1,3],[1,3].
点评:本题考查了复合函数的定义域问题,是一道中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
已知y=f(x)+x2是奇函数,且f(1)=1,若g(x)=f(x)+2,则g(-1)=( )
| A、-1 | B、0 | C、1 | D、2 |
在数列{an}中,a1=-
,an=1-
(n>1),则a2014的值为( )
| 1 |
| 4 |
| 1 |
| an-1 |
A、-
| ||
| B、5 | ||
C、
| ||
| D、以上都不对 |
若f′(x0)=-3,则
=( )
| lim |
| h→∞ |
| f(x0-3h)-f(x0) |
| h |
| A、-3 | B、-6 | C、9 | D、12 |
 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.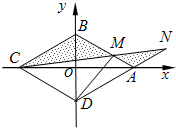 如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).
如图,菱形ABCD的边长为2,∠BAD=60°,M为AB边上不与端点重合的动点,且CM与DA分别延长后交于点N,若以菱形的对角线所在直线为坐标轴建立平面直角坐标系,并设BM=2t (0<t<1).