题目内容

若a＞b＞0，c＞d，则一定有（　　）
A、a+c＞b+d
B、a-c＞b-d
C、ac＞bd
D、
a
c
＞
b
d
考点：不等式的基本性质
专题：不等式的解法及应用
分析：利用不等式的基本性即可得出．
解答： 解：∵a＞b＞0，c＞d，
∴a+c＞b+d，
故选：A．
点评：本题考查了不等式的基本性，属于基础题．
练习册系列答案
相关题目
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两个焦点分别为F1（-2，0），F2（2，0），离心率e=
2

（Ⅰ）求双曲线的标准方程
（Ⅱ）点P是双曲线上一点，且∠F1PF2=30°，求△PF1F2的面积．
已知命题p：|x-a|＜3，q：（x-1）（4-x）＞0
（1）当a=1时，若“p且q”为真命题，求实数x的取值范围；
（2）若非p是非q的充分不必要条件，求实数a的取值范围．
如图所示的阴影部分﹙包括边界﹚对应的二元一次不等式组为（　　） 
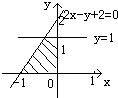
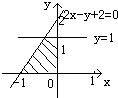
A、
0≤y≤1
x≤0
2x-y+2≥0
B、
y≤1
x≤0
2x-y+2≤0
C、
0≤y≤1
2x-y+2≤0
D、
y≤1
2x-y+2≤0
函数y=cosx在x∈[0，
π
6
]时的变化率为
 
；在x∈[
π
3
，
π
2
]时的变化率为
 
．
若有两个焦点F1，F2的圆锥曲线上存在点P，使|PF1|=3|PF2|成立，则称该圆锥曲线上存在“α”点，现给出四个圆锥曲线：①
x2
4
-
y2
12
=1  ②x2-
y2
15
=1  ③
x2
9
+
y2
7
=1  ④
x2
12
+
y2
4
=1，其中存在“α”点的圆锥曲线有（　　）
A、①③B、①④C、②③D、②④
设函数f（x）在（0，+∞）内可导，且f（ex）=x+ex，则f′（1）=（　　）
A、1B、2C、3D、4
求函数y=esinxln（tanx）的导数．
已知角α的终边过点P（3a-9，a+2），且cosα＜0，sinα＞0，求α的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网