题目内容
定义在R上的奇函数f（x）在（0，+∞）上的解析式为f（x）=x（
+1），则f（x）在（-∞，0）上的解析式为 ．
| 3 | x |
考点：函数奇偶性的性质,函数解析式的求解及常用方法
专题：计算题,函数的性质及应用
分析：由题意令设x∈（-∞，0），则-x∈（0，+∞）；从而由函数的奇偶性求解．
解答：
解：设x∈（-∞，0），则-x∈（0，+∞）；
又∵f（x）是R上的奇函数，
∴f（x）=-f（-x）
=-（-x（
+1））
=-x
+1；
故答案为：f（x）=-x
+1．
又∵f（x）是R上的奇函数，
∴f（x）=-f（-x）
=-（-x（
| 3 | -x |
=-x
| 3 | x |
故答案为：f（x）=-x
| 3 | x |
点评：本题考查了函数的奇偶性的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
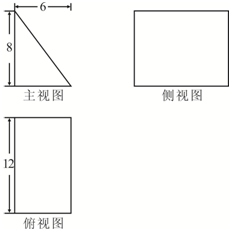一块橡胶泥表示的几何体的三视图如图所示，将该橡胶泥揉成一个底面边长为8的正三角形的三棱锥，则这个三棱锥的高为（ ）A、3
| ||
B、6
| ||
C、9
| ||
D、18
|