题目内容
已知p:|x-a|>
,q:2x2+9x-18<0,
(1)若?p是?q的充分不必要条件,求a的取值范围;
(2)若a=1,且p假q真,求x的取值范围.
| 3 |
| 2 |
(1)若?p是?q的充分不必要条件,求a的取值范围;
(2)若a=1,且p假q真,求x的取值范围.
考点:必要条件、充分条件与充要条件的判断,复合命题的真假
专题:简易逻辑
分析:(1)分别解出关于p,q的不等式,根据p,q之间的关系,从而求出a的范围;(2)把a=1代入,得到不等式,从而求出x的范围.
解答:
解:解不等式得:p:x<a-
或x>a+
,q:-6<x<
;
(1)∵?p是?q的充分不必要条件,
∴q是p的充分不必要条件,
∴不等式2x2+9x-18<0的解集是|x-a|>
的解集的子集,
∴a-
≥
或a+
≤-6,
即a≥3或a≤-
,
(2)当a=1时,p:x<-
或x>
,
则?p:-
≤x≤
,q:-6<x<
,
∴p假q真时x的范围是[-
,
).
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(1)∵?p是?q的充分不必要条件,
∴q是p的充分不必要条件,
∴不等式2x2+9x-18<0的解集是|x-a|>
| 3 |
| 2 |
∴a-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
即a≥3或a≤-
| 15 |
| 2 |
(2)当a=1时,p:x<-
| 1 |
| 2 |
| 5 |
| 2 |
则?p:-
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
∴p假q真时x的范围是[-
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了充分必要条件,考查了复合命题的真假问题,是一道基础题.

练习册系列答案
相关题目
给出如下性质:①最小正周期为π;②图象关于直线x=
对称;③在(-
,
)上是增函数.则同时具有上述性质的一个函数是( )
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
A、y=sin(
| ||||
B、y=cos(
| ||||
C、y=sin(2x-
| ||||
D、y=cos(2x+
|
不等式(x+1)(3-x)<0的解集是( )
| A、(-1,3) |
| B、(-∞,-1)∪(3,+∞) |
| C、(-3,1) |
| D、(-∞,-3)∪(1,+∞) |
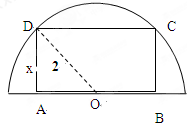 如图,有一块半径为2的半圆形钢板,计划剪裁成矩形ABCD的形状,设AD=x,矩形ABCD的面积为y,
如图,有一块半径为2的半圆形钢板,计划剪裁成矩形ABCD的形状,设AD=x,矩形ABCD的面积为y,