题目内容
已知函数f(x)是定义域为R的函数,且满足f(1)=2,f′(x)<f(x)+1,则不等式f(x)+1<3ex-1的解集为 .
考点:导数的运算,其他不等式的解法
专题:函数的性质及应用
分析:构造函数g(x)=
,利用导数研究其单调性即可得出.
| f(x)+1 |
| ex-1 |
解答:
解:构造函数g(x)=
,则g′(x)=
,
∵满足f(1)=2,f′(x)<f(x)+1,
∴g′(x)<0,
∴g(x)在R上单调递减,g(1)=f(1)+1=3.
∴不等式f(x)+1<3ex-1变为g(x)=
<g(1),
解集为{x|x>1}.
故答案为:{x|x>1}.
| f(x)+1 |
| ex-1 |
| f′(x)-f(x)-1 |
| ex-1 |
∵满足f(1)=2,f′(x)<f(x)+1,
∴g′(x)<0,
∴g(x)在R上单调递减,g(1)=f(1)+1=3.
∴不等式f(x)+1<3ex-1变为g(x)=
| f(x)+1 |
| ex-1 |
解集为{x|x>1}.
故答案为:{x|x>1}.
点评:本题考查了构造函数法、利用导数研究其单调性,考查了推理能力与计算能力,属于难题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
若向量
满足|
|=2,且向量
与向量
-
的夹角等
,则|
|的最大值为( )
| a |
| a |
| b |
| b |
| a |
| π |
| 6 |
| b |
| A、2 | ||||
| B、4 | ||||
C、2
| ||||
D、
|
已知向量
=({1,
),
=(3,m),若向量
与
的夹角为
,则实数m的值为( )
| a |
| 3 |
| b |
| a |
| b |
| π |
| 2 |
A、2
| ||
B、
| ||
| C、0 | ||
D、-
|
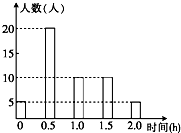 某校为了了解学生的课外阅读情况,随机抽查了50名学生,得到他们某一天各自课外阅读的时间数据如图所示,根据条形图可得到这50名学生该天每人的平均课外阅读时间为
某校为了了解学生的课外阅读情况,随机抽查了50名学生,得到他们某一天各自课外阅读的时间数据如图所示,根据条形图可得到这50名学生该天每人的平均课外阅读时间为