题目内容
已知集合A={1,2,3,4,5},用适当的符号填空:
①{1,2} A;
②3 A;
③{6} A;
④6 A.
①{1,2}
②3
③{6}
④6
考点:元素与集合关系的判断
专题:集合
分析:正确利用集合与元素,集合与集合之间的关系,尤其是符号使用恰当利用来逐个判断然后填空.
解答:
解:已知集合A={1,2,3,4,5},
①{1,2}与A是集合之间的关系,为A真子集,所以{1,2}?A,
②3是集合A中的元素,所以3∈A,
③{6}与A是集合间关系,且6∉A,所以{6}?A,
④6不是集合A中的元素,所以6∉A,
故答案为:?,∈,?,∉.
①{1,2}与A是集合之间的关系,为A真子集,所以{1,2}?A,
②3是集合A中的元素,所以3∈A,
③{6}与A是集合间关系,且6∉A,所以{6}?A,
④6不是集合A中的元素,所以6∉A,
故答案为:?,∈,?,∉.
点评:本题考查了元素与集合,集合与集合的关系,属于基础题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知A={x|0≤x≤3},B={y|0≤y≤3},下列从集合A到集合B的对应关系不是映射的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
已知m,n为异面直线,m?平面α,n?平面β,α∩β=l,则直线l( )
| A、与m,n都相交 |
| B、与m,n都不相交 |
| C、与m,n中至少一条相交 |
| D、至多与m,n中的一条相交 |
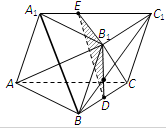 如图,在三棱柱ABC-A1B1C1中,D是BC的中点.
如图,在三棱柱ABC-A1B1C1中,D是BC的中点.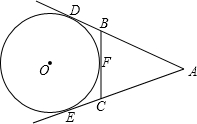 如图:AE、AD、BC分别切⊙O于E、D、F,若AD=14,则△ABC的周长为
如图:AE、AD、BC分别切⊙O于E、D、F,若AD=14,则△ABC的周长为