题目内容
6.若方程$\sqrt{4x-{x^2}}=\frac{3}{4}x+m$有实数解,则m的取值范围是[-3,1].分析 根据函数与方程之间的关系转化两个函数有交点问题,利用数形结合进行求解即可.
解答 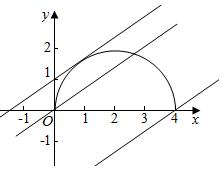 解:设y=$\sqrt{4x-{x}^{2}}$,则等价为(x-2)2+y2=4,(y≥0)对应的根据为圆的上半部分,
解:设y=$\sqrt{4x-{x}^{2}}$,则等价为(x-2)2+y2=4,(y≥0)对应的根据为圆的上半部分,
设y=$\frac{3}{4}$x+m,即3x-4y+4m=0
作出对应的图象如图:
当直线经过点(4,0)时,满足条件,
此时$\frac{3}{4}$×4+m=0,得m=-3,
当直线和圆相切时(m>0),
圆心到直线的距离d=$\frac{|6+4m|}{\sqrt{{3}^{2}+{4}^{2}}}=2$,
即$\frac{|3+2m|}{5}=1$,则|2m+3|=5
得m=1或m=-4(舍),
故要使方程$\sqrt{4x-{x^2}}=\frac{3}{4}x+m$有实数解,
则-3≤m≤1,
故答案为:[-3,1]
点评 本题主要考查函数与方程的应用,根据条件转化为直线和圆的位置关系是解决本题的关键.注意利用数形结合进行判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.某几何体的三视图如图所示,该几何体的侧面积( )
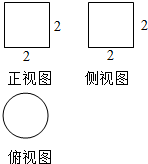

| A. | 5π | B. | 4π | C. | 3π | D. | 2π |
14.由函数y=ex,y=$\frac{e}{x}$,x=e所围成的封闭图形的面积为( )
| A. | ee-e | B. | ee-2e | C. | 2e-1 | D. | 1 |
18.已知点A(1,2,-1),点C与点A关于平面xOy对称,点B与点A关于x轴对称,则线段BC的长为( )
| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{7}$ |
15.有5个大小、质地都相同的小球,标号分别为1,3,5,7,9,从中任取三个小球,其标号之和能够被3整除的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
16.下列命题为真命题的是( )
| A. | 椭圆的离心率大于1 | |
| B. | 双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=-1$的焦点在x轴上 | |
| C. | $?x∈R,sinx+cosx=\frac{7}{5}$ | |
| D. | 不等式$\frac{1}{x}>1$的解集为(-∞,1) |