由函数y=ex.y=$\frac{e}{x}$.x=e所围成的封闭图形的面积为( )A．ee-eB．ee-2eC．2e-1D．1 题目和参考答案——青夏教育精英家教网—

题目内容

14．由函数y=e^x，y=$\frac{e}{x}$，x=e所围成的封闭图形的面积为（　　）

A．

e^e-e

B．

e^e-2e

C．

2e-1

D．

分析先求出两曲线的交点坐标（1，e），再由面积与积分的关系将面积用积分表示出来，由公式求出积分，即可得到面积值．

解答解：由e^x=$\frac{e}{x}$，可得x=1，
∴由函数y=e^x，y=$\frac{e}{x}$，x=e所围成的封闭图形的面积为${∫}_{1}^{e}$（e^x-$\frac{e}{x}$）dx=（e^x+$\frac{e}{{x}^{2}}$）${|}_{1}^{e}$=e^e-2e．
故选：B．

点评本题考查定积分在求面积中的应用，解答本题关键是根据题设中的条件建立起面积的积分表达式，再根据相关的公式求出积分的值，用定积分求面积是其重要运用，掌握住一些常用函数的导数的求法是解题的知识保证．

练习册系列答案

走进名校小学毕业升学模拟测试卷系列答案

全国68所名牌小学毕业升学真卷精编系列答案

5．

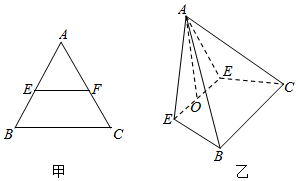如图甲，在边长为4的等边△ABC中，点E，F分别为AB，AC上一点，且EF∥BC，EF=2a，沿EF将△AEF折起，使得平面AEF⊥平面EFCB，形成一个如图乙所示的四棱锥，设O为EF的中点．
（1）求证：AO⊥BE；
（2）当a为何值时，四棱锥A-EFCB的体积最大，并求出最大值．

2．

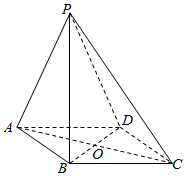如图，四棱锥P-ABCD底面ABCD为平行四边形，且AC∩BD=O，PA=PC，PB⊥BD，平面PBD⊥平面PAC．
（Ⅰ）求证PB⊥面ABCD；
（Ⅱ）若△PAC为正三角形，∠BAD=60°，且四棱锥P-ABCD的体积为$\frac{{\sqrt{6}}}{6}$，求侧面△PCD的面积．

9．已知向量$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$，$\overrightarrow{b}$=4$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$，其中$\overrightarrow{{e}_{1}}$=（1，0），$\overrightarrow{{e}_{2}}$=（0，1）．
（Ⅰ）试计算$\overrightarrow{a}$•$\overrightarrow{b}$及|$\overrightarrow{a}$+$\overrightarrow{b}$|的值；
（Ⅱ）求向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值．

19．圆C：（x+2）²+y²=32与抛物线y²=2px（p＞0）相交于A、B两点，若直线AB恰好经过抛物线的焦点，则p等于（　　）

6．若方程$\sqrt{4x-{x^2}}=\frac{3}{4}x+m$有实数解，则m的取值范围是[-3，1]．

3．

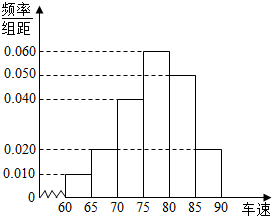2014年“双节”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段：[60，65），[65，70），[70，75），[75，80），[80，85），[85，90）后得到如图的频率分布直方图．
（1）求这40辆小型车辆车速的众数、平均数和中位数的估计值；
（2）若从车速在[60，70）的车辆中任抽取2辆，求车速在[65，70）的车辆恰有一辆的概率．

4．

根据如图程序框图，当输入5时，输出的是（　　）

试题分类