题目内容
16.下列命题为真命题的是( )| A. | 椭圆的离心率大于1 | |
| B. | 双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=-1$的焦点在x轴上 | |
| C. | $?x∈R,sinx+cosx=\frac{7}{5}$ | |
| D. | 不等式$\frac{1}{x}>1$的解集为(-∞,1) |
分析 A.根据椭圆离心率的性质进行判断.
B.根据双曲线的方程和性质进行判断.
C.根据三角函数的有界性进行判断.
D.根据不等式的解集进行判断即可.
解答 解:A.则椭圆中,a>c,∴椭圆的离心率e=$\frac{c}{a}$∈(0,1),故A错误,
B.双曲线$\frac{x^2}{m^2}-\frac{y^2}{n^2}=-1$的标准方程为$\frac{{y}^{2}}{{n}^{2}}-\frac{{x}^{2}}{{m}^{2}}$=1,则表示交点在y轴上,故B错误,
C.sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[$-\sqrt{2}$,$\sqrt{2}$],∵$\frac{7}{5}$∈[$-\sqrt{2}$,$\sqrt{2}$],
∴$?x∈R,sinx+cosx=\frac{7}{5}$成立,故C正确,
D.由$\frac{1}{x}>1$得0<x<1,故D错误,
故选:C.
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,难度不大.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
7.已知A(-1,2,1),B(1,3,4),则( )
| A. | $\overrightarrow{AB}$=(-1,2,1) | B. | $\overrightarrow{AB}$=(1,3,4) | C. | $\overrightarrow{AB}$=(2,1,3) | D. | $\overrightarrow{AB}$=(-2,-1,-3) |
4. 根据如图程序框图,当输入5时,输出的是( )
根据如图程序框图,当输入5时,输出的是( )
 根据如图程序框图,当输入5时,输出的是( )
根据如图程序框图,当输入5时,输出的是( )| A. | 6 | B. | 4.6 | C. | 1.9 | D. | -3.9 |
1.执行如图所示的程序框图,则输出S的值是( )
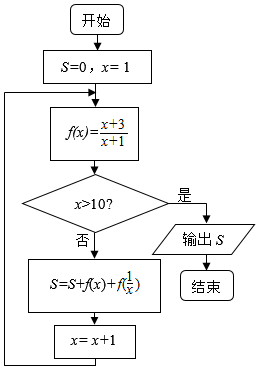

| A. | 36 | B. | 40 | C. | 44 | D. | 48 |
 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,以下四个命题:
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,以下四个命题: 函数f(x)=Asin(ωx+ϕ)(A,ω,ϕ是常数,且A>0,ω>0)的部分图象如图所示,下列结论:
函数f(x)=Asin(ωx+ϕ)(A,ω,ϕ是常数,且A>0,ω>0)的部分图象如图所示,下列结论: