题目内容
下列4个命题:
①“如果x+y=0,则x、y互为相反数”的逆命题;
②“如果x2+x-6≥0,则x>2”的否命题;
③在△ABC中,“A>30°”是“sinA>
”的充分不必要条件;
④“a=1”是“函数f(x)=(x-1)2在区间[a,+∞)上为增函数”的必要充分条件.
其中真命题的序号是 .
①“如果x+y=0,则x、y互为相反数”的逆命题;
②“如果x2+x-6≥0,则x>2”的否命题;
③在△ABC中,“A>30°”是“sinA>
| 1 |
| 2 |
④“a=1”是“函数f(x)=(x-1)2在区间[a,+∞)上为增函数”的必要充分条件.
其中真命题的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①写出“如果x+y=0,则x、y互为相反数”的逆命题,可判断①;
②写出“如果x2+x-6≥0,则x>2”的否命题,可判断②;
③利用充分必要条件的概念,举例A=160°>30°,但sin160°<
,可判断③;
④利用二次函数的对称性与单调性及充分必要条件的概念可判断④.
②写出“如果x2+x-6≥0,则x>2”的否命题,可判断②;
③利用充分必要条件的概念,举例A=160°>30°,但sin160°<
| 1 |
| 2 |
④利用二次函数的对称性与单调性及充分必要条件的概念可判断④.
解答:
解:①“如果x+y=0,则x、y互为相反数”的逆命题为“如果x、y互为相反数,则x+y=0”,是真命题;
②“如果x2+x-6≥0,则x>2”的否命题为“如果x2+x-6<0,则x≤2”,显然为假命题;
③在△ABC中,A>30°不能推出sinA>
,例如A=160°>30°,但sin160°<
,即充分性不成立,故③为假命题
④因为f(x)=(x-1)2在区间[a,+∞)上为增函数.
所以a≥1,
所以“a=1”是“函数f(x)=(x-1)2在区间[a,+∞)上为增函数”的充分不必要条件,故④为假命题.
故答案为:①.
②“如果x2+x-6≥0,则x>2”的否命题为“如果x2+x-6<0,则x≤2”,显然为假命题;
③在△ABC中,A>30°不能推出sinA>
| 1 |
| 2 |
| 1 |
| 2 |
④因为f(x)=(x-1)2在区间[a,+∞)上为增函数.
所以a≥1,
所以“a=1”是“函数f(x)=(x-1)2在区间[a,+∞)上为增函数”的充分不必要条件,故④为假命题.
故答案为:①.
点评:本题考查四种命题之间的关系及其真假判断,考查充分必要条件的概念及应用,基本知识的考查.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
在区间[-a,a](a>0)上,f(x)只是奇函数,g(x)只是偶函数,那么函数y=f(x)•g(x)( )
| A、只是奇函数 |
| B、只是偶函数 |
| C、既不是奇函数,也不是偶函数 |
| D、可能是奇函数,也可能是偶函数 |
设θ是第三象限的角,则点P(cosθ,tanθ)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
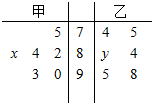 如图所示的茎叶图是甲乙两位同学咱期末考试中六科成绩,已知甲同学的平均成绩为85,乙同学的六科成绩的众数为84,则x,y的值为( )
如图所示的茎叶图是甲乙两位同学咱期末考试中六科成绩,已知甲同学的平均成绩为85,乙同学的六科成绩的众数为84,则x,y的值为( )| A、2,4 | B、4,4 |
| C、5,6 | D、6,4 |
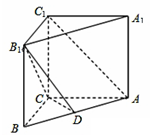 在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.